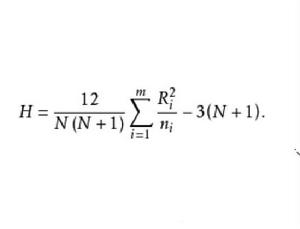基本介紹
克魯斯卡爾-沃利斯檢驗是一種秩檢驗，是威爾科克遜檢驗的推廣， 用於多個連續型獨立樣本的比較。方差分析(ANOVA)程式關注的是，幾個總體的均值是否相等。數據是間隔測量尺度或比率測量尺度的數據。另外還要假定這些總體服從正態機率分布，並且有相等的標準差。如果數據是順序測量尺度的和(或)總體不服從常態分配會怎樣呢?W.H.克魯斯卡爾(Kruskal)和W.A.沃利斯(Wallis)於1952年提出了僅僅要求順序(排序)測量尺度數據的非參數檢驗。不需要對總體分布形態做任何假定。該檢驗被稱為克魯斯卡爾-沃利斯單因素秩方差分析(Kruskal-Wallis one-way analysis of variance by ranks)。
為了利用克魯斯卡爾-沃利斯檢驗，從總體中抽取的樣本必須是獨立的。例如，從三個組(經理、員工、管理人員)中抽取樣本，並且進行訪談。一組人員(如經理)的回答決不能影響其他兩組的回答。
為了計算克魯斯卡爾-沃利斯檢驗統計量：①合併所有的樣本；②將合併後的樣本值從低到高排序；③將排序後的值用秩代替，從最小值1開始。
要套用方差分析技術，我們假定: (1) 總體都服從常態分配； (2) 這些總體有相等的標準差；(3) 樣本是獨立抽取的。如果這些假定都滿足，我們可以利用F分布作為檢驗統計量。如果這些假定不能被滿足，我們套用不依賴於分布的克魯斯卡爾-沃利斯檢驗 。
檢驗步驟
假設有m個相互獨立的簡單隨機樣本(X，…，X) (i=1，…， m) 。
檢驗步驟：
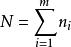克魯斯卡爾-沃利斯檢驗1)將各樣本全部 個觀測值按遞增順序排成一 列；
2)以R(i=1，…，m)表示第 i個樣本的n個觀測值X，…，X在此排列中的秩的和；
3) 計算統計量
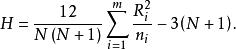克魯斯卡爾-沃利斯檢驗假如各樣本有r個相同數據，設t(i=1，…，r)是各樣本的第i個公共觀測值在全部N觀測值中出現 的次數，則計算如下修正統計量
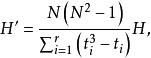克魯斯卡爾-沃利斯檢驗
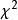克魯斯卡爾-沃利斯檢驗(當N充分大時H及H′近似服從 分布，自由度v=m-1)；
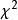克魯斯卡爾-沃利斯檢驗
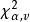克魯斯卡爾-沃利斯檢驗
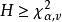克魯斯卡爾-沃利斯檢驗
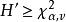克魯斯卡爾-沃利斯檢驗 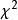克魯斯卡爾-沃利斯檢驗 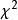克魯斯卡爾-沃利斯檢驗4)對於 給定的顯著性水平α和自由度v= m-1，由附表2查出 分布上側分位數 當 (或 )時，認為m個樣本不全來自同 一總體(無齊一性)，否則可以利用 機率積分表(附表1)計算檢驗的擬合優度 (參見“擬合優度 檢驗”)。
| v p c | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 22 24 26 28 30 | .3173 .1573 .0833 .0455 .0254 .0143 .0082 .0047 .0027 .0016 .0009 .0005 .0003 .0002 .0001 .0001 .0000 | .6065 .3679 .2231 .1353 .0821 .0498 .0302 .0183 .0111 .0067 .0041 . 0025 .0015 .0009 .0006 ，0003 .0002 .0001 .O001 .0000 .0000 .0000 .0000 .0000 .0000 | .8013 .5724 .3916 .2615 .1718 .1116 .0719 .0460 .0293 .0186 .0117 .0074 .0046 .0029 .0018 .0011 .0007 .0004 .0003 .0002 .0001 .0000 .0000 .0000 .0000 | .9098 .7358 .5578 .4060 .2873 .1992 .1359 .0916 .0611 .0404 .0266 .0174 .0113 .0073 .0047 .0030 .0019 .0012 .0008 .0005 .0002 .0001 .0000 .0000 .0000 | .9626 .8492 .7000 .5494 .4159 .3062 .2206 .1562 .1091 .0752 .0514 .0348 .0234 .0156 .0104 .0068 .0045 .0029 .0019 .0013 .0005 .0002 .0001 .0000 .0000 | .9856 .9197 .8089 .6767 .5438 .4232 .3209 .2381 .1736 .1247 .0884 .0620 .0430 .0296 .0203 .0138 .0093 .0062 .0042 .0028 .0012 .0005 .0002 .0001 .0000 | .9948 .9598 .8850 .7798 .6600 .5398 .4289 .3326 .2527 .1886 .1386 .1006 .0721 .0512 .0360 .0251 .0174 .0120 .0082 .0056 .0025 .0011 .0005 .0002 .0001 | .9983 .9810 .9344 .8571 .7576 .6472 .5366 .4335 .3423 .2650 .2017 .1512 .1119 .0818 .0592 .0424 .0301 .0212 .0149 .0103 .0049 .0023 .0011 .0005 .0002 |
(續)
| v p c | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 22 24 26 28 30 | .9994 .9915 .9643 .9114 .8343 .7399 .6371 .5342 .4373 .3505 .2757 .2133 .1626 .1223 .0909 .0669 .0487 .0352 .0252 .0179 .0089 .0043 .0020 .0010 .0004 | .9998 .9963 .9814 .9474 .8912 .8153 .7254 .6288 .5321 .4405 .3575 .2851 .2237 .1730 .1321 .0996 .0744 .0550 .0403 .0293 .0151 .0076 .0037 .0018 .0009 | .9999 .9985 .9907 .9699 .9312 .8734 .7991 .7133 .6219 .5304 .4433 .3636 .2933 .2330 .1825 .1411 .1079 .0816 .0611 .0453 .0244 .0127 .0065 .0032 .0016 | 1.0000 .9994 .9955 .9834 .9580 .9161 .8576 .7851 .7029 .6160 .5289 .4457 .3690 .3007 .2414 .1912 .1496 .1157 .0885 .0671 .0375 .0203 .0107 .0055 .0028 | 1.0000 .9998 .9979 .9912 .9752 .9462 .9022 .8436 .7729 .6939 .6108 .5276 .4478 .3738 .3074 .2491 .1993 .1575 .1231 .0952 .0554 .0311 .0170 .0091 .0047 | 1.0000 .9999 .9991 .9955 .9858 .9665 .9347 .8893 .8311 .7622 .6860 .6063 .5265 .4497 .3782 .3134 .2562 .2068 .1649 .1301 .0786 .0458 .0259 .0142 .0076 | 1.0000 1.0000 .9996 .9977 .9921 .9798 .9577 .9238 .8775 .8197 .7526 .6790 .6023 .5255 . 4514 .3821 .3189 .2627 .2137 .1719 .1078 .0651 .0380 .0216 .0119 |
當υ≥45時，使用近似公式：
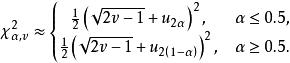克魯斯卡爾-沃利斯檢驗其中υ，是N(0，1) 的雙側分位數 。
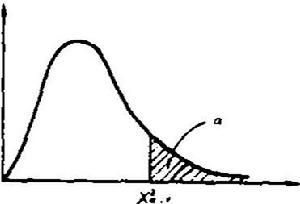圖1| α v | 0.995 | 0.990 | 0.975 | 0.95 | 0.90 | 0.70 | 0.50 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | 4×10 .010 .072 .207 .412 .676 .989 1.443 1.537 2.651 2.306 3.470 3.565 4.570 4.106 5.241 5.796 6.562 6.448 7.434 | 2×10 .020 .115 .297 .554 .872 1.239 1.646 2.088 2.558 3.053 3.571 4.107 4.660 5.229 5.812 6.408 7.015 7.633 8.260 | .001 .051 .216 .484 .831 1.237 1.690 2.180 2.700 3.247 3.816 4.404 5.009 5.629 6.262 6.908 7.564 8.231 8.907 9.591 | .004 .103 .352 .711 1.145 1.635 2.167 2.733 3.325 3.940 4.575 5.226 5.892 6.571 7.261 7.962 8.672 9.390 10.117 10.851 | .016 .211 .584 1.064 1.610 2.204 2.833 3.490 4.168 4.865 5.578 6.304 7.042 7.790 8.547 9.312 10.085 10.865 11.651 12.443 | .148 .713 1.424 2.195 3.000 3.828 4.671 5.527 6.393 7.267 8.148 9.034 9.926 10.821 11.721 12.624 13.531 14.440 15.352 16.266 | .455 1.386 2.366 3.357 4.351 5.348 6.346 7.344 8.343 9.342 10.341 11.340 12.340 13.339 14.339 15.338 16.338 17.338 18.338 19.337 |
(續)
| α v | 0.30 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | 1.074 2.408 3.665 4.878 6.064 7.231 8.383 9.524 10.656 11.781 12.899 14.011 15.119 16.222 17.322 18.418 19.511 20.601 21.689 22.775 | 2.706 4.605 6.251 7.779 9.236 10.645 12.017 13.362 14.684 15.987 17.275 18.549 19.812 21.064 22.307 23.542 24.769 25.989 27.204 28.412 | 3.841 5.991 7.815 9.488 11.070 12.592 14.067 15.507 16.919 18.307 19.675 21.026 22.362 23.685 24.996 26.296 27.587 28.869 30.144 31.410 | 5.024 7.378 9.348 11.143 12.832 14.449 16.013 17.535 19.023 20.483 21.920 23.336 24.736 26.119 27.488 28.845 30.191 31.526 32.852 34.170 | 6.635 9.210 11.345 13.277 15.086 16.912 18.475 20.090 21.666 23.209 24.725 26.217 27.688 29.141 30.578 32.000 33.409 34.805 36.191 37.566 | 7.879 10.597 12.838 14.860 16.750 18.548 20.278 21.955 23.589 25.188 26.757 28.300 29.819 31.319 32.801 34.267 35.718 37.156 38.582 39.997 | 10.828 13.816 16.266 18.467 20.515 22.458 24.322 26.125 27.877 29.588 31.264 32.909 34.528 36.123 37.697 39.252 40.790 42.312 43.820 45.315 |
(續)
| α v | 0.995 | 0.990 | 0.975 | 0.95 | 0.90 | 0.70 | 0.50 |
| 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | 8.430 8.346 9.062 9.688 10.025 11.061 11.808 12.461 13.121 13.787 14.458 15.134 15.815 16.01 17.192 17.887 18.586 19.289 19.996 20.707 21.421 22.138 22.859 23.584 24.311 | 8.897 9.542 10.196 10.856 11.524 12.198 12.879 13.565 14.256 14.953 15.655 16.362 17.073 17.789 18.509 19.233 19.960 20.691 21.426 22.164 22.906 23.650 24.398 25.148 25.901 | 10.283 10.982 11.688 12.401 13.120 13.844 14.573 15.308 16.047 16.791 17.539 18.291 19.047 19.806 20.569 21.336 22.106 22.878 23.654 24.433 24.215 25.999 26.785 27.575 28.366 | 11.591 12.338 13.091 13.848 14.611 15.379 16.151 16.928 17.708 18.493 19.281 20.072 20.867 21.664 22.465 23.269 24.075 24.884 25.695 26.509 27.326 28.144 Z8.965 29.787 30.612 | 13.240 14.041 14.848 15.659 16.473 17.292 18.114 18.939 19.768 20.599 21.434 22.271 23.110 23.952 24.797 25.643 26.492 27.343 28.196 29.051 29.907 30.765 31.625 32.487 33.350 | 17.182 18.101 19.021 19.943 20.867 21.792 22.719 23. 647 24.577 25.508 26.440 27.373 28.307 29.242 30.178 31.115 32.053 32.992 33.932 34.872 35.813 36.755 37.698 38.641 39.585 | 20.337 21.337 22.337 23.337 24.337 25.336 26.336 27.336 28.336 29.336 30.336 31.336 32.336 33.336 34.336 35.336 36.336 37.335 38.335 39.335 40.335 41.335 42.335 43.335 44.335 |
(續)
| α v | 0.30 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | 23.858 24.939 26.018 27.096 28.172 29.246 30.319 31.391 32.461 33.530 34.598 35.665 36.731 37.795 38.859 39.922 40.984 42.045 43.105 44.165 45.224 46.282 47.339 48.396 49.452 | 29.615 30.813 32.007 33.196 34.382 35.563 36.741 37.916 39.087 40.256 41.422 42.585 43.745 44.903 46.059 47.212 48.363 49.513 50.660 51.805 55.949 54.090 55.230 56.369 57.505 | 32.671 33.924 35.172 36.415 37.652 38.885 40.113 41.337 42.557 43.773 44.985 46.194 47.400 48.602 49.802 50.998 52.192 53.384 54.572 55.758 56.942 58.124 59.304 60.481 61.656 | 35.479 36.781 38.076 39.364 40.646 41.923 43.194 44.461 45.722 46.979 48.232 49.480 50.725 51.966 53.203 54.437 55.668 56.895 58.120 59.342 60.561 61.777 62.990 64.201 65.410 | 38.932 40.289 41.638 42.980 44.314 45.642 46.963 48.278 49.588 50.892 52.191 53.486 54.776 56.061 57.342 58.619 59.892 61.162 62.428 63.691 64.950 66.206 67.459 68.709 69.957 | 41.401 42.796 44.181 45.558 46.928 48.290 49.645 50.993 52.336 53.672 55.003 56.328 57.648 58.964 60.275 61.581 62.882 64.181 65.476 66.766 68.053 69.336 70. 616 71.893 73.166 | 46.797 48.268 49.728 51.179 52.618 54.052 55.476 56.892 58.301 59.703 61.098 62.487 63.870 65.247 66.619 67.985 69.346 70.703 72.055 73.402 74. 745 76.084 77.419 78.749 80.077 |
