相關概念
（1）泊松分布
泊松分布適合於描述單位時間內隨機事件發生的次數的機率分布。如某一服務設施在一定時間內受到的服務請求的次數，電話交換機接到呼叫的次數、汽車站台的候客人數、機器出現的故障數、自然災害發生的次數、DNA序列的變異數、放射性原子核的衰變數等等。
泊松分布的機率質量函式為：
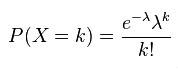克萊因羅克模型泊松分布的參數λ是單位時間(或單位面積)內隨機事件的平均發生率。
（2）指數分布
在機率論和統計學中，指數分布（Exponentialdistribution）是一種連續機率分布。指數分布可以用來表示獨立隨機事件發生的時間間隔，比如旅客進機場的時間間隔、中文維基百科新條目出現的時間間隔等等。
一個指數分布的機率密度函式是：
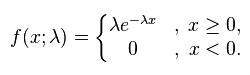克萊因羅克模型其中λ>0是分布的一個參數，常被稱為率參數（rateparameter）。即每單位時間發生該事件的次數。指數分布的區間是[0,∞)。如果一個隨機變數X呈指數分布，則可以寫作：X~Exponential（λ）。
原理
模型規定，網中任意兩節點j與k之間的通信只有一個路由。節點之間由兩條單向的鏈路連線，由j至k的鏈路，記作（J，k）；由k至j的鏈路則記作（k，j）。
圖中以一個三節點信息網為例，說明克萊因羅克模型的計算方法。
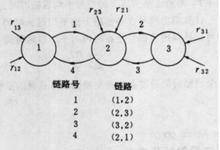圖1 三節點網
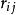克萊因羅克模型假設輸入的是泊松呼叫流。節點j用戶呼叫節點k的符號平均到達率（平均發生強度）為。用戶送至通信網的全部符號到達強度
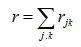克萊因羅克模型令λi為鏈路i上的符號平均到達率，它的值完全由相關的rjk和規定的路由所決定。何如，對於圖中的網路有
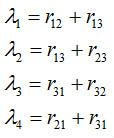克萊因羅克模型若符號長度服從平均值為1/μ（比特/符號）的指數分布．每個符號從一個節點向另一個節點傳送時，都將按照指數分布，以1/μ的平均值賦予新的符號長度。雖然這個假設不完全符合信息交換網的實際情況，但它卻簡化了理論計算，使該模型更容易套用於實際工程設計。這是克萊因羅克模型的一個主要特點。
計算
套用單線服務排隊系統理論，鏈路i上符號的平均遲延時間
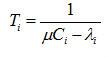克萊因羅克模型式中Ci為鏈路i的容量，單位為bit/s。對於實際系統，每條鏈路應滿足
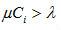克萊因羅克模型對於如圖所示的網路，遲延時間
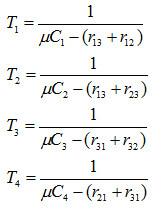克萊因羅克模型已知Ti,可以計算出各方向上符號的平均遲延時間。例如圖中節點l至節點3的符號平均遲延時間為T1+T2，節點2至節點3的符號平均遲延時間為T2。
計算得出符號在各鏈路上的平均遲延時間Ti後，還可以計算出全部符號在網內的平均遲延時間
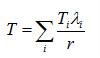克萊因羅克模型這個遲延時間是度量信息交換網服務質量的重要指標之一。
