基本介紹
 元電流
元電流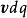 元電流
元電流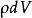 元電流
元電流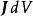 元電流
元電流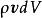 元電流
元電流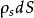 元電流
元電流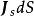 元電流
元電流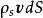 元電流
元電流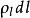 元電流
元電流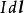 元電流
元電流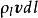 元電流
元電流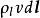 元電流
元電流如有元電荷以速度 運動,則 這一個量的單位為C·m/s=A·m,稱之為 元電流(段)。因此,可以得到作不同分布的元電荷運動後形成的元電流段。例如,與作體分布的元電荷 相應的元電流段為 等於 。與作面分布的元電荷 相應的元電流段為 等於 ,與作線分布的元電荷 相應的元電流段為 等於 ,或 。綜合上述,元電流有下列不同形式
 元電流
元電流畢奧-薩伐爾定律
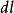 元電流
元電流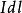 元電流
元電流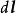 元電流
元電流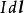 元電流
元電流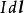 元電流
元電流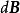 元電流
元電流靜電場中,在:計算任意帶電體在某點的電場強度時,曾採用 微元分割法,把帶電體分割成無限多個電荷元dq,每個電荷元dq 在場點產生的電場強度為d E,再疊加求和就可以得到帶電體在場點產生的電場強度 E。對於載流導線來說,可以仿此思路,把載流導線分成許多長度為 的電流元,電流元為矢量,大小為 ,方向沿導線上長度元 的方向,就是電流元處的電流方向,用矢量 表示。這樣,求出每個電流元 在空間某點產生的磁感應強度 ,再利用疊加理,就可得到載流導線在該點產生的磁感應強度 B。
1820 年10 月,法國物理學家畢奧(J.B.Biot) 和薩伐爾(F.Savart) 對不同形狀的載流導線所激發的磁場做了大量實驗研究,根據實驗結果分析得出了電流元產生磁場的規律。法國數學和物理學家拉普拉斯(P.S.Laplace) 將畢奧和薩伐爾得出的結果歸納為數學公式,總結出電流元產生磁場的規律一 畢奧-薩伐爾定律。其內容表述如下:
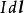 元電流
元電流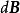 元電流
元電流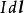 元電流
元電流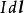 元電流
元電流 元電流
元電流 元電流
元電流電流元在空間某點P處產生的磁感應強度的大小與電流元的大小成正比,與電流元和電流元到P點的矢徑之間夾角的正弦sinθ成正比,而與電流元到P點的距離的平方成反比,數學表示式為:
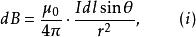 元電流
元電流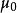 元電流
元電流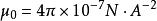 元電流
元電流其中,稱為真空磁導率,其值為
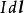 元電流
元電流 元電流
元電流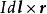 元電流
元電流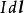 元電流
元電流 元電流
元電流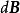 元電流
元電流d B的方向垂直於和組成的平面,並沿矢積的方向,其指向用右手螺旋定則確定,如圖2所示,右手四指由經小於180度的角轉向時,大拇指的指向即為的方向。
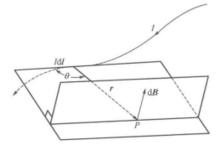 圖1 電流元激發的磁感應強度
圖1 電流元激發的磁感應強度這樣式(i) 就可寫成矢量式:
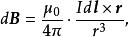 元電流
元電流上式就是 畢奧-薩伐爾定律。這是計算電流磁場的基本公式。根據磁場的疊加原理,任意載流導線在P點產生的磁感應強度 B為
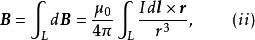 元電流
元電流式中積分是對整個載流導線進行積分。
式(ii) 為矢量式,套用時通常要化為標量式。需指出,畢奧-薩伐爾定律是根據大量實驗事實分析得出的結果,無法用實驗直接驗證。然而由該定律出發得出的結果卻與實驗符合得很好,這間接地驗證了該定律的正確性 。
元電流所受的力
一個帶電粒子在磁場中運動所受到的力可以表示成如下一個元電荷所受到的微元力
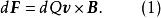 元電流
元電流從物理上來看,元電荷是由許多占據著一定體積的非常小的和離散的電荷所組成,儘管這些電荷所占的體積很小,但是比之各個電荷之間的平均距離卻要大得多。這樣,式(1)所表示的微元力僅僅是作用在各個離散電荷上的力的總和,而不是作用在某一單個離散電荷上的力。採用相似的方法,我們也可以分析一陣落沙中的一小撮沙子所受到地球引力的微元重力。在這一小撮沙子中包含了許多沙粒,而微元重力就是作用在一小撮沙子中每個沙粒上的力的總和 。
然而,如果電荷是在導體中運動的電子,我們可以證明作用在導體上的力就是這些電子所受到的力,這些量值極小卻又數量極多的力的總和是有重要實際意義的。在導體內部,每個電子都是在某個正離子附近的有限固定區域內運動的,這些正離子構成了一個晶格陣列並確定了導體自身的固體特性。磁場施加給電子的作用力趨於使電子作微小的移動,使得在正電荷和負電荷兩者的重心之間產生一個小的位移。然而,電子和正離子之間存在的庫侖力卻企圖阻止這種位移的發生。因此,任何使電子移動的企圖都將會在電子和晶格陣列中的正離子之間引起吸引力。這樣,磁場力就被轉移到晶格陣列上或導體自身上。在良導體中,由於庫侖力遠遠大於磁場力,所以電子的實際位移幾乎是不可能測量出來的。然而,在導體實驗樣品兩端出現的一個微小電位差卻表明了磁場力使電荷被分離,該電位差沿垂直於磁場和電荷運動速度兩者的方向。這個電位差稱為 霍耳電壓,把這個效應稱為 霍耳效應。
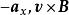 元電流
元電流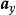 元電流
元電流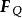 元電流
元電流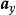 元電流
元電流 元電流
元電流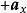 元電流
元電流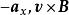 元電流
元電流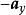 元電流
元電流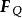 元電流
元電流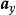 元電流
元電流在圖2中分別示出了對於運動正電荷和負電荷的霍耳電壓的方向。在圖2(a)中,由於 v的方向為 的方向為 ,Q是正電荷,所以力 的方向為 ;這樣正電荷向右邊移動。在圖2(b)中,速度 現在的方向為 , B的方向仍然為 方向則為 ,Q是負電荷,所以力 的方向仍然是 。此時,負電荷也向右邊移動。因此,在半導體中由空穴和電子所產生的兩個相等的電流可以由它們的霍耳電壓來加以區分。這就是確定一給定半導體究竟是p型還是n型半導體的一種方法。
 圖2(a)
圖2(a) 圖2(b)
圖2(b)圖2(a)中進入紙面的正電荷與(b)中流出紙面的負電荷形成了兩個相等的電流。如圖所示,這兩種情況可以由相反取向的霍耳電壓來加以區分。
利用霍耳效應可以製作測量磁通密度的儀表以及可以用做電子功率計、矩形脈衝元件等,在這些套用中可以使得流過儀表的電流與其中存在的磁場成正比。
若再看一看式(1),我們可以說如果現在分析的是電子束中一個運動的電荷元,則力僅僅是這個小體積元中每個電子所受力的總和,但是如果現在分析的是導體中一個運動的電荷元,則總力是作用在這個導體自身上的。
電流密度定義為體電荷密度與其速度的乘積,
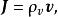 元電流
元電流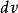 元電流
元電流而在式(1)中的元電荷也可以用體電荷密度來表示( 是一個體電荷元而並不是速度的一個微分增量),
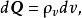 元電流
元電流這樣
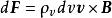 元電流
元電流或
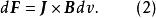 元電流
元電流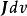 元電流
元電流把 可以解釋成一個電流元;也就是說,
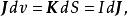 元電流
元電流這樣,就可以把洛倫茲力方程套用於面電流密度,
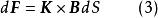 元電流
元電流或套用於一個細線電流元,
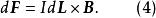 元電流
元電流對式(2)、式(3)或式(4)分別在某一體積內、某一曲面(可以是非閉合的,也可以是閉合的,為什麼?)上或在某一閉合路徑上進行積分,可以得到以下積分公式
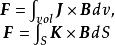 元電流
元電流和
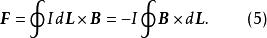 元電流
元電流把式(4)或式(5)套用於在均勻磁場中的一段直導線,可以得到一個簡單的結果:
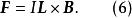 元電流
元電流利用熟悉的公式,可以得到這個力的大小為
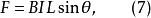 元電流
元電流 元電流
元電流其中, 是電流流動方向的矢量與磁通密度方向之間的夾角。式(6)或式(7)僅僅適用於在閉合迴路中的一部分,在實際問題中則必須考慮迴路中餘下的另外一部分 。