簡介
儒科夫斯基變換是指通過解析變換z=1/2(す+b²/す)(b為常數),將輔助平面面す=ε+iη上的簡單物面變換為物理平面z=x+iy上較複雜物面的保角變換方法。儒科夫斯基變換在理論和實踐上都具有重大價值 。
儒科夫斯基變換的性質
根據解析變換唯一性定理,儒科夫斯基變換具有下述性質:
①除分支點z=±b處不保角(dz/dす=0)外,其他各處都具有保角性。
②す平面上的圓|す|=b,變換成z平面上的平板,則平面上的圓柱繞流可變換為z平面上的平板繞流。
③す平面上的圓|す|=a(a>b),變換為z平面上的橢圓。
④す平面上す=±b兩點在虛軸上有偏心距f1的的偏心圓,變換為z平面上最大彎度為f1、無厚度過z=±b兩點的圓弧。
⑤過す=+b點在實軸上有偏心距す(<0)的偏心圓,變換為厚度與|r|有關、無彎度過x=b點的儒科夫斯基對稱翼型。
⑥過す=b點的偏心圓,變換為過z=b點的儒科夫斯基凹形翼型,除後緣點B處不保角外,處處保角,翼型的翼弦主要決定於b,而f1、r1與翼型的彎度、厚度有關 。
示意圖
儒科夫斯基變換性質原理圖如圖1所示 :
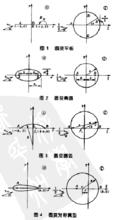 圖1
圖1方法
求儒科夫斯基翼型繞流的方法首先是利用儒科夫斯基變換。分別將物理平面上的平板、橢圓、圓弧翼型、儒科夫斯基對稱翼型及凹形翼型等變換為輔助平面上的圓 。