基本概念
基於函式逼近論,將一組傅立葉基函式作為三層前向神經網路各隱含神經元的輸出特性,以其加權和作為網路的非線性輸出,構成一種新型的傅立葉神經網路,從理論上解決了單輸入神經網路隱含層數及隱含神經元個數難以確定的問題。
以一組傅立葉基函式作為三層前向神經網路各隱含層單元的輸出特性,再以其加權和作為網路的非線性輸出,即可構成一種傅立葉神經網路模型。由於神經元的空間整合具有多樣性,從傅立葉神經網路可知,一個傅立葉神經網路就是一個傅立葉級數,反過來,一個傅立葉函式對應著一個傅立葉神經網路;從傅立葉函式套用的角度來看,可根據工程實際需要,構造出各種類型的傅立葉神經網路模型 。
傅立葉級數
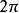 傅立葉神經網路
傅立葉神經網路周期為 的函式f(x),若能展開成三角級數:
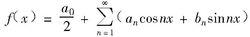 傅立葉神經網路
傅立葉神經網路式(1)
則稱之為函式f(x)的傅立葉級數,簡稱傅氏級數。
在工程實際中,各種複雜的振動現象是由不同頻率、不同振幅的簡諧振動迭加而成的,即一個複雜的波形可以分解為一系列諧波的線性組合;從函式逼近角度考慮,也就是說,任意一個函式可以展開成傅立葉級數。但函式f(x)未知時,因展開式中的係數難以計算,可以利用神經網路的自適應學習功能,對該未知函式的一組觀測樣本進行訓練,達到辨識目的。
下面是兩個基本定理。
定理1
若f(x)在(-l,l)內逐段連續並有逐段連續的導數,且一切不連續點ξ是正則的,即
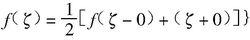 傅立葉神經網路
傅立葉神經網路則f(x)可展開成傅氏級數:
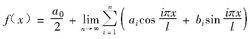 傅立葉神經網路
傅立葉神經網路式(2)
式中
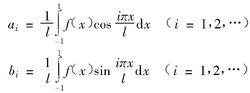 傅立葉神經網路
傅立葉神經網路定理2
若f(x)在[-l,l]上平方可積,則f(x)的傅氏級數均方收斂於f(x)。
傅立葉神經網路模型
若將正交三角函式系
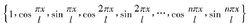 傅立葉神經網路
傅立葉神經網路式(5)
作為三層前向神經網路各隱含神經元的活躍函式,傅氏係數作為隱層至輸出層的聯接權值,則網路的輸出特性正是(2)式的部分和。故定理1從理論上證明了傅立葉神經網路必為三層前向網路,且隱含神經元的個數為2n+1,此即(5)式中基函式的個數。
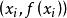 傅立葉神經網路
傅立葉神經網路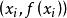 傅立葉神經網路
傅立葉神經網路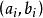 傅立葉神經網路
傅立葉神經網路針對工程實際情況,f(x)未知,僅知 的一組觀測值,採用神經網路學習算法,根據 搜尋一組傅氏係數 ,從而構成傅立葉神經網路。
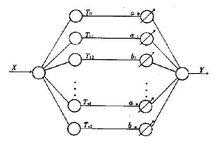 傅立葉神經網路
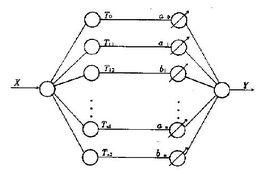
傅立葉神經網路圖1
圖1是一個傅立葉神經網路模型,其輸入層至隱層聯接權值恆為1,隱層至輸出層聯接權值為一組傅氏係數。網路操作特性如下:
(1)輸入單元O=x
(2)隱單元輸出為一組傅立葉基函式(正交三角函式系)
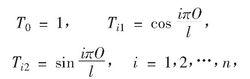 傅立葉神經網路
傅立葉神經網路(3)輸出單元
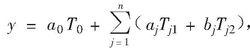 傅立葉神經網路
傅立葉神經網路(4)在輸入模式作用下,網路輸出值y與理想值法f(x)的誤差:
 傅立葉神經網路
傅立葉神經網路為樣本點個數。
(5)訓練指標:
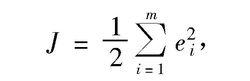 傅立葉神經網路
傅立葉神經網路(6)權值修正:
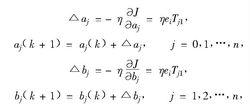 傅立葉神經網路
傅立葉神經網路0<η<1為學習率 。