簡介
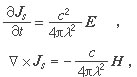 倫敦方程
倫敦方程倫敦方程是F.倫敦(Fritz London 1900~1954)和H.倫敦(Heinz London 1907~19
70)所建立的超導體的電動力學方程,成功地解釋了超導體一系列奇特的電磁性質。
內容
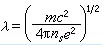 倫敦方程
倫敦方程超導體中的電子由兩部分組成,一部分仍與普通導體中的電子相同,稱為正常電子,遵從歐姆定律;另一部分具有超導電性,運動時不受任何阻力,稱為超導電子。1935年倫敦兄弟根據超導體的這兩個基本性質,提出描述超導電子運動規律的方程:
式中JS是超導電流,C是光速,右式稱為倫敦穿透深度,ns是超導電子的密度,m、e為電子的質量和電荷。如果是直流電流,由方程(1)可直接得出電阻率為零,因此方程(1)反映了理想導電性的事實。由方程(2)可得出在超導體表面附近,磁場是按指數規律衰減的。穿透層的深度約為λ,其數量級為10-16cm。在超導體內部磁場為零。因此方程(2)反映了理想抗磁性的事實。
倫敦方程預言了表面透入層的存在。而且當超導體的尺寸與λ相近時,磁場會透入到樣品中心。因此小尺寸超導體不具有完全抗磁性,它在磁場中的能量就比大塊超導體低,從而臨界磁場會高於大塊樣品。
另一方面,實驗發現,對於錫、銦等超導體,λ的測量值以及臨界磁場與樣品尺寸的關係,與倫敦理論只是定性的符合,在數量上並不一致,有的甚至定性的關係也不符合。
倫敦第一方程
倫敦第一方程說明超導電流的時間變化率由電場決定。它表明了靜場時超導體內電場為零,概括了零電阻效應。
※倫敦第二方程
這一方程說明超導電流與磁場的關係。它說明:
1.超導電流是有鏇的,可以在一環形迴路中形成持續的超導電流。2.由這個方程可以證明,Js和B都只存在於超導體表面層內,即有邁斯納效應稱為穿透深度。
※倫敦方程的修正-Pippard非局域理論
JS與A(r)的非局域關係-Pippard方程:
其中,
並且假設
為純淨超導體的相干長度(本徵相干長度),l為電子的平均自由程
