概念
在統計物理中的郎之萬方程,應該是隨機微分方程,而且不是普通意義下的隨機微分方程
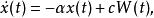 伊藤積分
伊藤積分 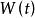 伊藤積分
伊藤積分 代表布朗粒子所受到的隨機力,它被視為一個白噪音過程。由於白噪音不是一個普通的隨機過程,所以,朗之萬方程的嚴格數學表達遇到了困難。
更一般地,考慮方程
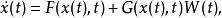 伊藤積分
伊藤積分 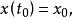 伊藤積分
伊藤積分 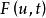 伊藤積分
伊藤積分 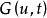 伊藤積分
伊藤積分 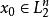 伊藤積分
伊藤積分 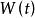 伊藤積分
伊藤積分  伊藤積分
伊藤積分 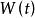 伊藤積分
伊藤積分 其中 與 是兩個確定性函式, , 是 維白噪音過程。由於 不是普通隨機過程,故上式雖然是有重要實際意義的,但卻沒有嚴格的數學意義。
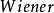 伊藤積分
伊藤積分 注意到白噪音過程是作為 過程的導過層是引入的,因而上式在形式上等價於方程
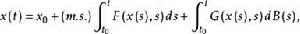 伊藤積分
伊藤積分 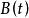 伊藤積分
伊藤積分  伊藤積分
伊藤積分 是 過程。
上式比較容易賦以嚴格的定義,只須對其右端第二個積分加以解釋罷了。我們可以把第二個積分理解為斯蒂爾吉斯均方積分
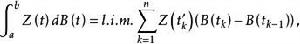 伊藤積分
伊藤積分 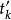 伊藤積分
伊藤積分 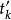 伊藤積分
伊藤積分 不幸的是,等式右端的極限差不多總是不存在的。伊藤解決了這一困難,他把 點的取法作了限制, 永遠取子區間的左端點
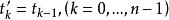 伊藤積分
伊藤積分 這樣規定的積分,就是有名的伊藤積分。
基本原理
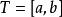 伊藤積分
伊藤積分 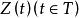 伊藤積分
伊藤積分 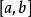 伊藤積分
伊藤積分 定義:設 , 是隨機過程,對 區間取一划分
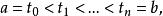 伊藤積分
伊藤積分 求和
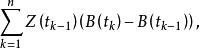 伊藤積分
伊藤積分 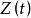 伊藤積分
伊藤積分 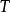 伊藤積分
伊藤積分 若無限分細時,此和式有唯一的均方極限,則稱該極限為 在 上的伊藤積分,記作
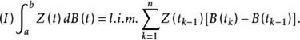 伊藤積分
伊藤積分 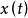 伊藤積分
伊藤積分 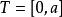 伊藤積分
伊藤積分 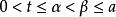 伊藤積分
伊藤積分 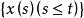 伊藤積分
伊藤積分 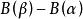 伊藤積分
伊藤積分 定理:若在上連續,對任意,都有與獨立,則
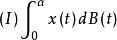 伊藤積分
伊藤積分 存在。
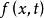 伊藤積分
伊藤積分 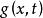 伊藤積分
伊藤積分 定理:設與是兩個實函式,滿足
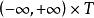 伊藤積分
伊藤積分 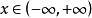 伊藤積分
伊藤積分  伊藤積分
伊藤積分 (1)都在上連續,且對每一,關於一致連續。
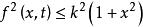 伊藤積分
伊藤積分 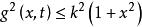 伊藤積分
伊藤積分 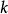 伊藤積分
伊藤積分 (2),,其中為一常數。
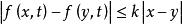 伊藤積分
伊藤積分 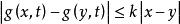 伊藤積分
伊藤積分 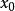 伊藤積分
伊藤積分 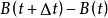 伊藤積分
伊藤積分 (3)李普西茲條件:,,又設與任意獨立,則伊藤方程有唯一確定的解。
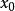 伊藤積分
伊藤積分 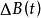 伊藤積分
伊藤積分 定理:設與任意獨立,則伊藤方程的解是一個馬爾科夫過程。

