定義
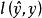代理損失函式在二元分類問題中，假如我們有n個訓練樣本{(X1,y1),(X2,y2),⋯,(Xn,yn)}，其中yi∈{0,1}。為了量化一個模型的好壞，我們通常使用一些損失函式，損失函式越小，模型越好。最常用的損失函式就是零一損失函式。
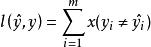代理損失函式對於一損失函式l，目標是要找到一個最優的分類器h，使得這個分類器在測試樣本上的期望損失最小。數學式子表達是：
代理損失函式
代理損失函式理論上，我們是可以直接對上式進行最佳化，得到最優的分類器h。然而這個過程是非常困難的（甚至不可行）。其一是因為X×y的機率分布是未知的，所以計算loss的期望是不可行的。另外一個難處是這個期望值很難進行最佳化，因為這個損失函式是非連續的，這個最佳化問題本質是NP-Hard的。舉個例子來說，假定，我們希望找一個線性分類器
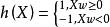代理損失函式
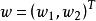代理損失函式
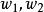代理損失函式使得loss的期望最小化。所以也就是求解。關於以及loss的圖像大致如下：
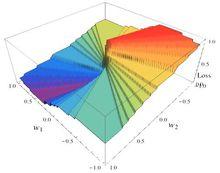w1,w2與loss的關係圖這個函式顯然是非連續的。常用的最佳化方法，比如梯度下降，對此都失效了。正因此，可以考慮一個與零一損失相接近的函式，作為零一損失的替身。這個替身就稱作代理損失函式（surrogate loss function） 。
性質
如果最最佳化代理損失函式的同時也最最佳化了原本的損失函式，就稱校對性(calibration)或者一致性(consistency)。這個性質與所選擇的代理損失函式相關。一個重要的定理是，如果代理損失函式是凸函式，並且在0點可導，其導數小於0，那么它一定是具有一致性的 。
零一損失函式與logloss，hinge loss，squared hinge loss以及modified Huber loss的聯繫如下圖：
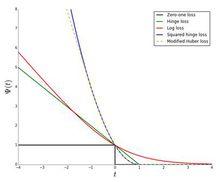零一損失函式與logloss，hinge loss等的聯繫