生平
早年生活
亨利·歐內斯特·杜德尼出生於英格蘭,蘇塞克斯郡,梅菲爾德的一個村莊,是全家六個孩子中的老二。他的父親吉爾伯特·杜德尼(Gilbert Dudeney)約1825年出生於梅菲爾德,是一位校長。而他的祖父,約翰·杜德尼(John Dudeney)以牧羊人的身份起家,是一位自學成才的業餘數學家與天文學家,之後成為劉易斯一所學校的校長。他的自學精神被孫輩們所敬仰。亨利的母親,露西·安·里奇(Lucy Ann Rich)約1832年出生於薩默塞特郡的布里奇沃特。亨利有一個哥哥托馬斯(Thomas,約1855),以及四個妹妹,分別是露西(Lucy,約1862)、凱特(Kate,約1863)、艾米麗(Emily,約1864)和愛麗絲(Alice,約1865)。
亨利·杜德尼年輕時就開始學習西洋棋,並很快著迷於象棋問題,這也成為了他一生的愛好。無疑,象棋激起了小亨利對於數學與謎題的強烈愛好。從九歲開始,他就開始在當地報紙上發表自己創作的謎題。雖然他僅僅接受過一些基礎教育,並且沒有上過大學,但他對數學有強烈的愛好並在自己的業餘時間學習數學以及數學史。
幾何
平面分割
幾何圖形的平面分割問題是要求將多邊形分割成儘可能少的塊數來拼成另一種指定的幾何圖形。根據由偉大的德國數學家希爾伯特(David Hilbert)最早證明的一個定理,任何一個多邊形都可以通過分割成有限數量的小塊,來轉換成等面積的另一種多邊形。儘管希爾伯特的方法可以保證把一種多邊形分割成有限數量的小塊來轉換成另一種多邊形,但需要的小塊數量很大。要將這件事完成得簡潔一些,則要求分割的塊數儘可能少,這往往是極難確定的。杜德尼在這種古怪的幾何學藝術上取得了極大的成就,常常比長期保持的紀錄高出一籌。
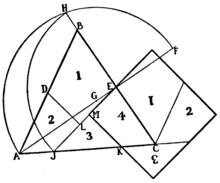 正三角形轉換為正方形的方法圖示
正三角形轉換為正方形的方法圖示杜德尼最著名的幾何學發現就是把一個等邊三角形剪成四塊,然後拼成一個正方形。這道問題以”縫紉用品商的趣題“的名字出現在《坎特伯雷趣題集》中。切割的方法是這樣的,根據附圖,取AB的中點D,取BC的中點E;延長直線AE至F,使EF等於EB;取AF的中點G,以G為圓心作弧AHF;延長EB至H,EH就是所求正方形的邊長;以E為圓心,EH為半徑,作弧HJ,再使JK等於BE;由D、K兩點作EJ的垂線,交EJ於L和M。 切割即告完畢,可以用這四塊拼成一個標準的正方形。需要注意的是點J和點K並不位於點D和點E的正下方。
 三角形轉換的動態演示
三角形轉換的動態演示杜德尼於1905年5月17日將這個問題在伯靈頓大廈向皇家學會作了報告,又於下一個月在皇家科學研究所作了報告,採用的是更一般的形式:”一個新的圖形重合問題:證明一個等邊三角形可被分割成四塊,然後重新拼合成一個正方形,附關於一種將所有直線三角形通過剖分變換成正方形的一般方法的幾個例子。”如另一幅圖所示,把四個小塊在三個頂點處相接,就形成一個鏈,按順時針方向閉合就是一個三角形,按逆時針方向閉合則是一個正方形。杜德尼把這個圖形用紅木和銅鉸鏈製成模型,在倫敦皇家學會的會議上做演示。
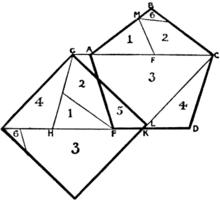 正五邊形轉換正方形圖示
正五邊形轉換正方形圖示多年以來人們一直認為將正五邊形轉換為正方形至少得分割成七塊才行,這是由數學家保羅·畢曉普(Paul Busschop)做出的解答。杜德尼把這個數字成功地降到了六。他的解答是先形成一個平行四邊形,由此再形成正方形。在《數學中的娛樂》一書中,他說明了分割的方法:正五邊形為ABCDE。通過切割AC和切割FM(F是AC的中點,M與A的距離等於F與A的距離),得到兩個切割塊,可以放到GHEA的位置上,形成平行四邊形GHDC。然後求出這平行四邊形的邊長HD和高的比例中項。由此標定K點,使C到K的距離等於這個比例中項。連線CK,由G作KC的垂線GL。餘下的事情很顯然,這六個切割塊既可以拼成正五邊形,也可以拼成正方形。
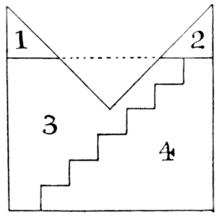 主教冠形轉換為正方形的兩種解法
主教冠形轉換為正方形的兩種解法杜德尼的一些趣題與同時期的美國趣題天才薩姆·勞埃德(Sam Loyd)的作品相同,顯然這兩位趣題專家都毫不猶豫地參考和修改對方的發明。在勞埃德的著作《趣題大全》中記載了這樣一道剖分趣題:要求將一個主教冠形(正方形缺四分之一)分割成儘可能少的塊數,再拼成一個正方形。勞埃德提出了一種解法,使用了所謂的台階原理:將塊1和塊2割下拼在三角形空檔中,以形成一個矩形。利用台階原理,將塊4下移一個台階,即可形成正方形。 但杜德尼提出這其實是個錯誤的解法,並給出了自己的正解:虛線為輔助線,AB是BD的一半,而AE平行於BH。以B為圓心作弧HE,AE將等於從B到C的距離。於是FG等於BC減去AB。用五塊可以拼成一個正方形。而且杜德尼堅信不存在只用四塊的解。
數論
立方和問題
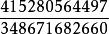 亨利·杜德尼
亨利·杜德尼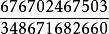 亨利·杜德尼
亨利·杜德尼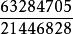 亨利·杜德尼
亨利·杜德尼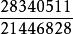 亨利·杜德尼
亨利·杜德尼在杜德尼的諸多涉及數論的難題中,最難解的也許要數《坎特伯雷趣題集》里一位醫生提出的問題。這位心靈手巧的醫生製作了兩個球形的藥瓶,一個周長剛好1英尺,另一個周長2英尺。他說:“我希望知道,另外兩個藥瓶的準確尺寸(即用有理數表示),它們的形狀與這兩個相似,但大小不同,而且它們合起來可以盛得下與這兩個藥瓶等量的藥水。”相似立體的體積之比與其相應線度的立方成正比,由此可知,因為這兩個藥瓶的周長分別是一英尺和兩英尺,而1的立方和2的立方相加得9,所以此題即是要求另外兩個有理數的立方和等於9。杜德尼的解答是: 和 。這兩個分數的立方和恰好是9,而這兩個分數的分母比任何以前發表過的分數的分母都要短。杜德尼在沒有現代計算機的條件下,能取得這樣的成就令人驚嘆。杜德尼還指出如果兩個藥瓶的周長分別是一英尺和三英尺,則有這樣一個答案: 和 ,其立方和為28。
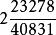 亨利·杜德尼
亨利·杜德尼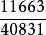 亨利·杜德尼
亨利·杜德尼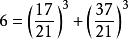 亨利·杜德尼
亨利·杜德尼在《坎特伯雷趣題集》中,杜德尼還設計了一道類似的問題:要求找到兩個有理數,其立方和為17。對於這道題,杜德尼評論道:“這是一根硬骨頭,只有那些自信有高智商的人才可嘗試。”他的解答用了儘可能少的數碼,分別是 和 。杜德尼評論道:“我們對於到100為止的任何數,除66外,都可以說出它是否可以表示為兩個有理數的立方和。”法國數學家勒讓德曾經用相當篇幅“證明”了6不可能被表示為兩個有理數的立方和,而杜德尼發現了一個簡單解: 。 但杜德尼後來發現,盧卡斯(François Édouard Anatole Lucas)在與西爾維斯特(James Joseph Sylvester)的一次通信中已經在他之前得到了這個解。
著作
| 書名 | 原書名 | 出版日期 | 備註 |
| 坎特伯雷趣題集 | The Canterbury Puzzles | 1907 | 插圖者: P. Hardy |
| 數學中的娛樂 | Amusements in Mathematics | 1917 | |
| 世界上最好的文字謎題 | The World's Best Word Puzzles | 1925 | |
| 現代趣題 | Modern Puzzles | 1926 | |
| 謎題及其它古怪的問題 | Puzzles and Curious Problems | 1931 | 逝世後出版 |
| 謎題寶藏 | A Puzzle-Mine | 193? | 逝世後出版 |

