交替最小二乘法

在矩陣分解（matrix factorization）中使用的一種算法。有一個稀疏矩陣，假設這個矩陣是低階的，可以分解成兩個小矩陣相乘。然後交替對兩個小矩陣使用最小二乘法，算出這兩個小矩陣，就可以估算出稀疏矩陣缺失的值。與坐標下降法有點相似。

算法內容

假設

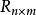交替最小二乘法

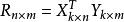交替最小二乘法

假設要對一個低階的稀疏矩陣 進行矩陣分解，使得 。

損失函式

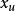交替最小二乘法

交替最小二乘法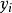

交替最小二乘法

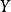交替最小二乘法

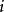交替最小二乘法

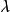交替最小二乘法

交替最小二乘法

交替最小二乘法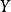

交替最小二乘法

設 為矩陣 的第 個列向量， 為矩陣 的第 個列向量。有最小二乘錯誤加上正則化項的損失函式 ，其中 為參數。只要求損失函式最小時的 和 即可。

偽代碼

交替最小二乘法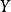

交替最小二乘法

初始化 和

repeat

for u=1...n do

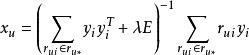交替最小二乘法

end for

for i=1...m do

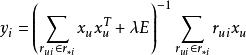交替最小二乘法

end for

until循環足夠次數

套用

常用於推薦算法。