基本介紹
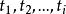交叉子樣本
交叉子樣本 交叉子樣本如果在隨機抽樣時不止抽一個樣本，而是按同樣的抽樣方法抽取兩個或兩個以上的小樣本，這些小樣本根據研究問題的目的可以是獨立地抽取，也可以不獨立地抽取，這些抽取的小樣本稱之為 交叉子樣本。設是k個獨立的交叉子樣本對總體參數的無偏估計值，那么所有交叉子樣的平均數也是的無偏估計量。即：
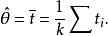交叉子樣本
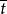交叉子樣本而的方差為：
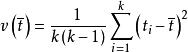交叉子樣本是估計量方差的無偏估計，計算比較簡單。當k=2時，方差的公式可簡化為：
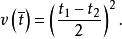交叉子樣本這種交叉子樣本的方法最初用於總體參數的估計，以後又擴大套用於估計抽樣和非抽樣誤差等 。
在分層抽樣與多階段抽樣中，要抽取容量為n的一個樣 本。假定有k個調查員，則將樣本隨機分為k個部分——子樣本，子樣本容量為m=n/k。周密計畫安排使每個調查員至少在兩個層次或兩個群類上獨立隨機地抽取m個抽樣單位進行交叉調查，這k個容量為m的子樣本，稱做 交叉子樣本。交叉子樣本主要用於確定抽樣誤差中， 由於調查人員的誤差和回答錯誤所產生的，計量誤差的相關部分和這部分占總誤差的比例。
相關介紹
交叉子樣本這個方法是馬哈拉諾比斯(1946年)所建議的，它對研究相關的誤差特別有用。用最簡單的話語來介紹，這個方法就是把一個包含n個單位的隨機樣本隨機地劃分為k個子樣本，每個子樣本包含m=n/k個單位。對樣本的現場調查工作和數據處理工作進行了周密的計畫，使各不同子樣本中任何兩個單位的計量誤差之間沒有相關。
當把交叉方法套用到包括廣闊地理區域的多級樣本中時，最通常的做法是採用一對對的調查員，對從逐級最小的群中抽取的交叉子樣本進行計量。這樣調查員被指定要調查的最終單位數仍保持調查中的習慣水平，儘管調查員必須走過的地區面積是通常地區面積的兩倍。
美國普查局(1968年)曾在回答方差研究中採用這種形式的交叉方法。對1960年普查項目的總回答方差的相關分量進行了估計。這一研究中的區域是分布在整個美國的整群住戶。在任何一個樣本群中都有兩個交叉子樣本，每個子樣本指定由不同的一個調查員去凋查。
交叉方法是能在分層抽樣與多級抽樣中推廣套用的。我們確信，各不同子樣本中的計量誤差是相互獨立的，嚴格地說，這就要求在各不同的子樣本中採用不同的調查員，不同的監督員與不同的數據處理員。
這一方法有時稱為重複抽樣(replicated sampling)。戴明曾經廣泛地採用過。他在1960年曾敘述過這一方法的許多套用·：對於這一方法的優點的其他討論請見瓊斯(Jones)(1955車)巧庫普(1960年)的論文。採用交叉方法之後， 調查員的差旅費用增加了，但如果把樣本分層為一些完整的地區，這一缺點是可以減輕的，例如，每個層可以包含兩個隨機樣本，指派一個不同的調查員去調查，要求每個調查員在整個層中跑動，而不是只在半個層中跑動 。
