背景
隨著傳統能源的日益枯竭和環境污染的不斷加劇,開發可再生的清潔能源已經成為全世界面臨的共同課題。 在各種形式的新能源開發中,利用太陽能來發電的光伏技術備受矚目,但光伏發電作為社會整體能源結構的組成部分所占比例尚不足1%, 造成這種狀況的主要原因是光伏發電的成本太高。 所以,降低發電成本是目前光伏技術面臨的首要任務,有效途徑之一是採用聚光太陽電池,用比較便宜的菲涅耳透鏡聚光器來部分代替昂貴的太陽電池,這就是所謂的聚光型光伏技術。
採用聚光型光伏技術的高倍聚光光伏模組都需要配備高精度的雙軸跟蹤系統。 但是,由於雙軸跟蹤系統的跟蹤誤差會大大降低聚光太陽電池接收到的光能量。 同時,由於菲涅耳透鏡高倍聚焦光斑的熱點效應、聚光太陽電池對光斑強度分布均勻性的依賴性以及系統安裝精度的限制,高倍聚光光伏系統的轉換效率會受到很大限制。 因此,世界上多個研發機構都在考慮把二次聚光器引入聚光系統。 並且,無論是軟體模擬還是實際套用,結果都表明:二次聚光器對系統效率的提高有著重要的意義。
二次聚光器聚光原理
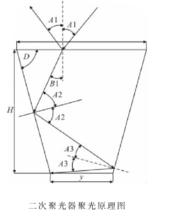 二次聚光器
二次聚光器二次聚光器實質上是一個倒置的玻璃稜錐。 右圖是它的二維聚光光路圖,光線從上底面折射進入全反射式二次聚光器,經過兩個側面的全反射入射到下底面, 由於上底面面積大於下底面面積,所以,它可以起到二次聚光的作用。
由折射定律和三角幾何關係可知:
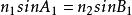 二次聚光器
二次聚光器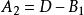 二次聚光器
二次聚光器 二次聚光器
二次聚光器式中: n 、 n 分別為空氣和二次聚光器材料的折射率。
為了保證光能透過率需要使光線在側壁全反射,根據全反射定律可知:
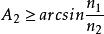 二次聚光器
二次聚光器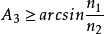 二次聚光器
二次聚光器綜合上述五個公式得:
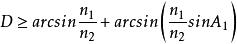 二次聚光器
二次聚光器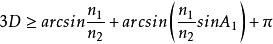 二次聚光器
二次聚光器由上兩個公式可確定入射角 A 和傾角 D 的關係,從而對全反射式二次聚光器的設計提供理論依據。 對於存在更多次全反射的情況,可以根據上述方法進行推導。而對於更複雜的三維聚光以及多波長聚光的情況,則需要結合光學設計軟體的光線追跡來進行仿真設計。
設計原則
全反射式二次聚光器是安裝在菲涅耳透鏡和太陽電池之間起連線作用的光學元件,上底面位於菲涅耳透鏡的焦平面 , 下底面緊貼著太陽電池。 為了不造成太陽電池的浪費,二次聚光器出射面的形狀和大小要跟太陽電池一致。 為了不造成光能量的浪費,它的入射面形狀跟出射面形狀一致,大小由菲涅耳透鏡聚焦光斑的大小和跟蹤系統的跟蹤誤差角度來決定。 然後由理論分析的結果確定初始高度,再通過非成像光學光線追跡不斷最佳化,直到太陽電池表面獲得最高的理想光學效率和光斑強度分布均勻性。
性能分析
對光斑強度分布均勻性的分析
由於太陽電池串聯電阻焦耳效應的存在,非均勻的光斑強度分布會降低太陽電池的填充因子。 而太陽電池的轉換效率公式為:
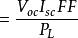 二次聚光器
二次聚光器η
式中:
 二次聚光器
二次聚光器P——表示太陽光入射能量;
V——表示開路電壓;
I——表示短路電流;
FF ——表示填充因子。
由上式可知,提高填充因子可以提高太陽電池的光電轉換效率。
如右圖,在沒有二次聚光器的情況下,菲涅耳透鏡在太陽電池表面上形成的光斑強度分布均勻性為 0.91% ,引入二次聚光器後在太陽電池表面形成的光斑強度為 90.24% ,可見二次聚光器的引入大大提高了光斑強度分布的均勻性,進而提高電池的轉換效率。
對跟蹤誤差容忍度的分析
 二次聚光器
二次聚光器目前,比較成熟的雙軸跟蹤系統的跟蹤精度都可以控制在 0.5° 以內。 但是對於高倍聚光光伏系統,光線的稍微偏移都會引起聚焦光斑的大距離偏移,從而在太陽電池表面上產生很大的光能量損失。右圖上表示在跟蹤誤差為 0.5° 時單菲涅耳透鏡在太陽電池表面上形成的能量分布情況。 右圖下為引入二次聚光器後在太陽電池表面上形成的能量分布情況。
在跟蹤系統的跟蹤誤差為 0.5° 時,引入二次聚光器之前, 太陽電池表面接收到了入射光能量的 86.6% ,而在引入二次聚光器後,太陽電池表面接收到了入射光能量的 98.5% ,二次聚光器的引入使太陽電池表面上接收的能量提高了大約 12% 。
可見,在跟蹤系統的跟蹤誤差為 0.5° 時,二次聚光器的引入可以使太陽電池接收到的光能量仍保持在 98% 以上, 而在沒有二次聚光器的情況下,太陽電池只能接收到大約 87% 的光能量。 所以,二次聚光器能提高系統接收角,降低對跟蹤系統跟蹤精度的要求。

