定義
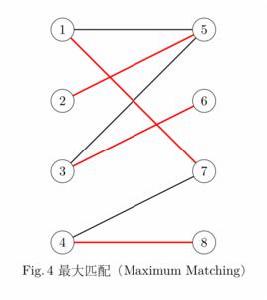
極大匹配(Maximal Matching)是指在當前已完成的匹配下,無法再通過增加未完成匹配的邊的方式來增加匹配的邊數。最大匹配(maximum matching)是所有極大匹配當中邊數最大的一個匹配。選擇這樣的邊數最大的子集稱為圖的最大匹配問題。
如果一個匹配中,圖中的每個頂點都和圖中某條邊相關聯,則稱此匹配為完全匹配,也稱作完備匹配。
求二分圖最大匹配可以用最大流(Maximal Flow)或者匈牙利算法(Hungarian Algorithm)
圖
設G=(V,E)是一個圖,M是E的一個子集,如果M不含環且任意兩邊都不相鄰,則稱M為G的一個匹配。G中邊數最多的匹配稱為G的最大匹配。 對於圖G=(V,E),在每條邊e上賦一個實數權w(e)。設M是G的一個匹配。定義 M中所有邊權值之和稱之為匹配M的權。G中權最大的匹配稱為G的最大權匹配。如果對一切,e∈E,w(e)=1,則G的最大權匹配就是G的最大匹配。
匹配
設M是圖G=(V,E)的一個匹配,vi∈V。若vi與M中的邊相關聯,則稱vi是M飽和點,否則稱vi為M非飽和點。 如果G中每個頂點都是M飽和點,則稱M為G的完美匹配。 設M是G的一個匹配,P是G的一條鏈。如果P的邊交替地一條是M中的邊,一條不是M中的邊,則稱P為M交錯鏈。類似地,我們可以定義G的交錯圈。易知,G的交錯圈一定是偶圈。 一條連線兩個不同的M非飽和點的M交錯鏈稱為M增廣鏈。 兩個集合S1與S2的“異或”操作S1⊕S2是指集合S1⊕S2=(S1∩S2)-(S1∪S2) 容易看出,設M是G的匹配,P是G中的M增廣鏈、則M⊕P也是G的匹配,而且 可以證明,G中匹配M是最大匹配若且唯若G中沒有M增廣鏈。
例題
中、日、韓三個足球隊進行比賽,已知A不是第一名,B不是韓國隊,也不是第二名,第一名不是日本隊,中國隊第二.問A、B、C各代表哪國隊?各是第幾名?
我們先來降低難度.先只要求你判斷出中、日、韓各是第幾名(不必判斷A、B、C).可以把中、日、韓各用一個點代表,列於上一行.第一、二、三名各用一個點代表,列於下一行,記為:
V1={中,日,韓},V2={第1名,第2名,第3名}.
V1中的點與V2中某一個點有肯定關係的,就畫一條實線,如和②.否定關係的兩點之間畫一條虛線,如不是②;不是①.把已知條件不加任何推理地表現於圖上.虛線2條,實線1條,共3條線.
現在,有兩個明顯的事實;第一,V1中每點有且只有一條實線與V2中相應點配對,V2中每點有且只有一條實線與V1中相應點配對.V1內部點之間不會有線相聯結,V2內部點之間也不會有線相聯結.第二,從V1(或V2)中某一個點,例如說a點如發出了一條實線向著V2(或V1)中某一個點,例如說x點,那么a點與V2(或V1)中其他點之間必然只能用虛線聯結.(這是邏輯推理中的排它性)
由此,我們很容易將中、日、韓的名次判出.
這樣的問題,抽象起來可歸屬於圖論中稱之為“二分圖的匹配”問題.
圖論的名詞術語太多,這裡不作詳細定義,只是描述性介紹一下,大家以前在“一筆畫”等講中已初步接觸.所謂二分圖,就是頂點集合可以劃分成兩個部分,V=V1+V2,如V1有p個點,記為V1={v1,v2…,vp},V2有q個點,記為V2={vp+1,vp+2…,vp+q},而V1中任意一點,不會與V1中其他點聯結,而只能與V2中某些點聯結;V2也如此.大家看幾個例.
一般的圖記為G=(V,E),V是頂點集合,E是邊(也可稱為線)的集合.大家在哥尼斯堡七橋問題中已領略過這種抽象.現在的二分圖是一類特殊的圖,只不過頂點集V劃分為兩部分,而這只能“跨越”於V1中某個點和V2中另一個點.二分圖的匹配問題,就是找一個邊的集合,這些邊之間都沒有公共的端點.
關於二分圖的匹配,要研究的是“最大匹配”,即找一個邊最多的匹配.
就本講開始引入的問題看,我們還沒有解完,因為還有A、B、C三個代號到底如何歸於中、日、韓三隊的問題.一種解題辦法,是把已判出的國籍和名次捆綁在一個頂點內,如(中2)、(韓1)、(日3),再和A、B、C構造一個新的二分圖:
顯然,推知B是(日3),因為B有2條虛線,而必然有1條實線,只能推出B與(日3)之間為實線.同理,(韓1)只能為C;剩下的唯一的情況留給了A為(中2).全部問題解決了.
再看最初的題目,如果你選擇先判斷中、日、韓和A、B、C三個代號之間的匹配關係,將會怎樣呢?畫一個圖看,利用已知條件畫出實、虛線.
只能利用B不是韓國隊及中國隊第二,B不是第二(因此B不是中國隊)這樣一些條件,題目中另二句話:A不是第一名,第一名不是日本隊,這種否定關係之間,沒有傳遞性,你不能判定A是不是日本隊.因此根據已知條件所畫的圖中只有兩條虛線,之後最多只能確定日、B之間為實線.所以對這樣的二分圖,無法找出合理的最大匹配.這方法使問題求解走進了死胡同.
那么你選擇先判A、B、C和第一、第二、第三名之間的匹配關係,又會怎樣呢?畫一個圖看.
現在也只有二條虛線,仍然無法找出最大匹配,或說解不唯一,對求解問題無助.
現在回過頭來看,先找國別與名次之間的匹配,似乎有些“碰運氣”,因為完全可以把題目改動,使先找國別與名次的匹配無法解決,例如敘述改為:
中、日、韓三足球隊比賽,已知結果為:第1名不是A,第2名不是韓國隊也不是B,A不是日本隊,中國隊為B,問A、B、C,和1、2、3名與各國隊如何匹配?
細心讀者發現,這只是把原題中A、B、C的地位與1、2、3名的地位互換而已.所以現在改動後的題目,再先抓“國別”和“名次”的匹配,就無法求解.
但是數學要求找出一種解一般問題的方法而不是“碰運氣”,而且完全可以找一個例子,使得無論取國別與名次;或國別與代號(A,B,C);或代號與名次這三類二分圖的匹配都無法求解,而必須找更廣泛意義下的匹配才能解決,為此先介紹一般的三個因素一起考慮的“匹配”方法.
先結合前例,將國別用三個不同點表示於上方,三個名次點表示於左下方,三個代號點表示於右下方.用實線的肯定關係和虛線的否定關係把已知條件“翻譯”於圖上.