基本概念
二元決策圖(binary decision diagram, BDD)是一種基於Shannon分解的有向無環圖,最早由Sheldon B.Akers於1978年提出的,它實質上是簡化布爾函式的Shannon分結束得到的。BDD是被用來表達一個布爾函式的一種數據結構。
二元決策圖的描述
BDD是一種基於Shannon分解的有向無環圖,最早由Sheldon B.Akers於1978年提出。設f是一組布爾變數集合X的布爾函式,且x為集合X中的變數,則Shannon分解及其if-then-else(ite)形式為:
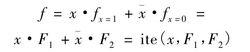 二元決策圖
二元決策圖 二元決策圖
二元決策圖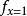 二元決策圖
二元決策圖 二元決策圖
二元決策圖式中x和分別代表,事件發生和不發生;(即F1)和(即F2)分別表示x發生和不發生的布爾函式。
BDD用二叉樹形式表示布爾邏輯函式:
 二元決策圖
二元決策圖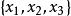 二元決策圖
二元決策圖 二元決策圖
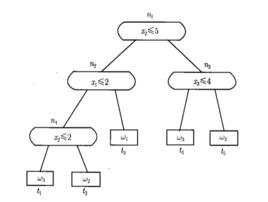
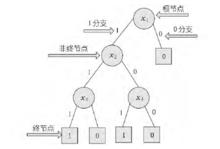
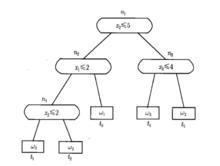
二元決策圖BDD是個有向無環圖,包含終節點和非終節點,節點之間靠1或0分支連線。終節點分兩種狀態,1和0分別表示兩種不交的邏輯狀態即系統或部件的失效狀態和正常狀態。非終節點對應故障樹的基本事件,每個非終節點的1分支代表基本事件失效,0分支代表基本事件正常。自BDD的根節點向下遍歷直到到達一個終節點,整條路徑構成一條BDD的通路,必然結束在0或1狀態之一,分別表示頂事件不發生和發生,而終節點為1的路徑中的節點構成系統的割集。圖中BDD示例所表示的頂事件發生的最小割集為到達終節點1的所有路徑,即,。
決策樹與二叉樹
決策樹
決策樹(又稱樹分類器或分類樹)是模式識別中進行分類的一種有效方法。利用樹分類器可以把一個複雜的多類別分類問題轉化為若干個簡單的分類問題來解決。它不是企圖用一個決策規則把多個類別的樣本一次分開,而是採用分級的方法,使分類問題逐步得到解決。總結起來,決策樹就是一個將輸入空間逐步分割的過程,它把輸入空間分為一組互不相交的子區域,其中某個類別的樣本占有優勢的區域標記為該樣本的類別。
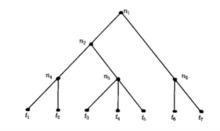
決策樹示意圖如下:
 二元決策圖
二元決策圖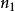 二元決策圖
二元決策圖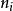 二元決策圖
二元決策圖 二元決策圖
二元決策圖一般地,一個決策樹由一個根節點,一組非終止節點和一些終止節點(也稱葉節點、葉子)構成,每個葉節點標以相應的樣本類別標籤,不同的葉節點可以有相同的類別標籤。
二叉樹
決策樹的一種簡單形式是二叉樹,二叉樹結構的分類器可以把一個複雜的多類別分類問題化為多級、多個兩類問題來解決,在每個節點都把樣本集分為左右兩個子集。分出的每個部分任然可能包含多個類別的樣本,在下一級的節點,把每個部分再分為兩個子集,依此進行,直到最後分出的每個部分只包含同一類別的樣本,或某一類別樣本占優勢為止。
優點:概念簡單、直觀,便於解釋。在各個節點上可以選擇不同的特徵和採用不同的決策規則。
二叉樹示意圖如下:
 二元決策圖
二元決策圖二元決策圖分析故障樹
採用BDD方法分析故障樹,不需求解最小割集就可以得出頂事件發生機率,能夠簡化故障樹定性和定量分析過程。
故障樹向BDD轉化
一個普遍的採用的構建BDD的方法是對故障樹中每個門結構套用if-then-else(ite)規則。轉化的遞歸算法思路是:從故障樹最底層基本事件開始,用ite結構進行轉化,用基本事件替換邏輯門,形成新的ite結構,然後繼續向上一層進行ite結構轉化,使得新的邏輯門都被基本事件替換,如此逐步向上,直到所有的邏輯門都被基本事件替換,則頂事件的BDD形成。
 二元決策圖
二元決策圖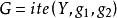 二元決策圖
二元決策圖構建BDD過程中,先對故障樹基本事件排序,然後對故障樹中每個門結構進行BDD轉化。令F和G分別表示BDD中的2個節點,其中,,轉化規則如下:
如果在故障樹基本事件排序中,X位於Y的前面,即X<Y,則:
 二元決策圖
二元決策圖如果X=Y,則:
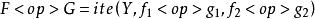 二元決策圖
二元決策圖式中,<op>是故障樹中邏輯門(AND或OR)的布爾運算元 。
基本步驟
典型的FT分析BDD方法的流程如下:
(1)FT結構預處理,結構簡化,並進行模組化;
(2)將獨立模組轉化成相應的BDD結構,求解最小割集,進行定量分析;
(3)將各個獨立模組看作初始故障樹的底事件,求解最小割集;
(4)進行疊代,得到最終的最小割集,作定量分析。