九階幻方

九階幻方 每行、每列、兩條對角線之和相等（都是369）

Merzirac法生成

在第一行居中的方格內放1，依次向右上方填入2、3、4…，如果右上方已有數字，則向下移一格繼續填寫。如下圖用Merziral法生成的9階幻方：

47 58 69 80 1 12 23 34 45

57 68 79 9 11 22 33 44 46

67 78 8 10 21 32 43 54 56

77 7 18 20 31 42 53 55 66

6 17 19 30 41 52 63 65 76

16 27 29 40 51 62 64 75 5

26 28 39 50 61 72 74 4 15

36 38 49 60 71 73 3 14 25

37 48 59 70 81 2 13 24 35

9階幻方的幻和值為369。

Merzirac法，有人也叫樓梯法，我管它叫斜步法，即走X+Y斜步（數字按右上方順序填入），-Y跳步（如果右上方已有數字或出了對角線，則向下移一格繼續填寫）。

其實斜步法可以向4個方向依次填寫數字，即右上、右下、左上、左下4個方向，每種斜步都可有2種跳步，即左（右）跳步、上（下）跳步。

對於X+Y斜步相應的跳步可以為-X，-Y。 【記住，跳步是X+Y斜步的X（或Y）相反方向即可。如右上方向斜步，跳步就為向左（或向下）一步；左下方向斜步，跳步就為向右（或向上）一步；等等等等】

loubere法生成

在居中的方格向上一格內放1，依次向右上方填入2、3、4…，如果右上方已有數字，則向上移兩格繼續填寫。如下圖用Louberel法生成的9階幻方：

77 28 69 20 61 12 53 4 45

36 68 19 60 11 52 3 44 76

67 27 59 10 51 2 43 75 35

26 58 18 50 1 42 74 34 66

57 17 49 9 41 73 33 65 25

16 48 8 40 81 32 64 24 56

47 7 39 80 31 72 23 55 15

6 38 79 30 71 22 63 14 46

37 78 29 70 21 62 13 54 5

上述loubere法可以記作X+Y斜步（數字按右上方順序填入），2Y跳步（如果右上方已有數字或出了對角線，則向上移二格繼續填寫）。對於X+Y斜步相應的跳步可以為2X，2Y。 【記住，跳步是X+Y斜步的X（或Y）相同方向即可。】

2Y跳步，則在居中的方格向上一格放1里，按上斜步，2Y跳步的方法構成幻方。

-2Y跳步，則在居中的方格向下一格放1里，按下斜步，-2Y跳步的方法構成幻方。

2X跳步，則在居中的方格向右一格放1里，按右斜步，2X跳步的方法構成幻方。

-2X跳步，則在居中的方格向左一格放1里，按左斜步，-2X跳步的方法構成幻方。

horse法生成

對於所有的奇階幻方，在第一行居中的方格內放1，向右走1步，下走2步以跳馬步，依次填入2、3、4…，若出到方陣下方，把該數字填到本該填數所在列上方相應的格；若出到方陣右方，把該數字填到本該填數所在行的左方相應的格；如果落步格已有數字， 則向下移一格繼續填寫。如下圖用Horse法生成的9階幻方：

77 58 39 20 1 72 53 34 15

6 68 49 30 11 73 63 44 25

16 78 59 40 21 2 64 54 35

26 7 69 50 31 12 74 55 45

36 17 79 60 41 22 3 65 46

37 27 8 70 51 32 13 75 56

47 28 18 80 61 42 23 4 66

57 38 19 9 71 52 33 14 76

67 48 29 10 81 62 43 24 5

集團方陣法

將n階幻方等分成m×m個k階幻方（m，k≥3），用數由小到大完成每一個k階幻方，將每一個k階幻方依次當成m階幻方中的1至m^2的數，再以這m^2個小k階幻方,以m階幻方的方法去完成大的m階幻方，從而完成n階幻方。

71 64 69 8 1 6 53 46 51

66 68 70 3 5 7 48 50 52

67 72 65 4 9 2 49 54 47

26 19 24 44 37 42 62 55 60

21 23 25 39 41 43 57 59 61

22 27 20 40 45 38 58 63 56

35 28 33 80 73 78 17 10 15

30 32 34 75 77 79 12 14 16

31 36 29 76 81 74 13 18 11

橫豎錯位補角

1.在九階表格中按順序填入1~81

1	2	3	4	5	6	7	8	9
10	11	12	13	14	15	16	17	18
19	20	21	22	23	24	25	26	27
28	29	30	31	32	33	34	35	36
37	38	39	40	41	42	43	44	45
46	47	48	49	50	51	52	53	54
55	56	57	58	59	60	61	62	63
64	65	66	67	68	69	70	71	72
73	74	75	76	77	78	79	80	81

2.橫錯位（左低右高）

								1	2	3	4	5	6	7	8	9
							10	11	12	13	14	15	16	17	18
						19	20	21	22	23	24	25	26	27
					28	29	30	31	32	33	34	35	36
				37	38	39	40	41	42	43	44	45
			46	47	48	49	50	51	52	53	54
		55	56	57	58	59	60	61	62	63
	64	65	66	67	68	69	70	71	72
73	74	75	76	77	78	79	80	81

3.橫補角

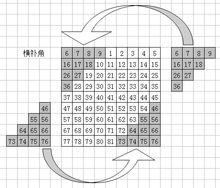九階幻方

得到

6	7	8	9	1	2	3	4	5
16	17	18	10	11	12	13	14	15
26	27	19	20	21	22	23	24	25
36	28	29	30	31	32	33	34	35
37	38	39	40	41	42	43	44	45
47	48	49	50	51	52	53	54	46
57	58	59	60	61	62	63	55	56
67	68	69	70	71	72	64	65	66
77	78	79	80	81	73	74	75	76

4.豎錯位（左低右高）

								5
							4	15
						3	14	25
					2	13	24	35
				1	12	23	34	45
			9	11	22	33	44	46
		8	10	21	32	43	54	56
	7	18	20	31	42	53	55	66
6	17	19	30	41	52	63	65	76
16	27	29	40	51	62	64	75
26	28	39	50	61	72	74
36	38	49	60	71	73
37	48	59	70	81
47	58	69	80
57	68	79
67	78
77

5.豎補角

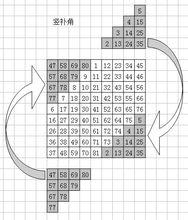九階幻方

得到結果。（結果1.左低右高，先橫後豎）

47	58	69	80	1	12	23	34	45
57	68	79	9	11	22	33	44	46
67	78	8	10	21	32	43	54	56
77	7	18	20	31	42	53	55	66
6	17	19	30	41	52	63	65	76
16	27	29	40	51	62	64	75	5
26	28	39	50	61	72	74	4	15
36	38	49	60	71	73	3	14	25
37	48	59	70	81	2	13	24	35

總結：此法要求兩次錯位所得傾斜方向必須一致，同是“左低右高”，或同是“左高右低”，橫豎可先可後。最後可得出4種基本結果。

結果2.左低右高，先豎後橫

15	25	35	45	46	56	66	76	5
34	44	54	55	65	75	4	14	24
53	63	64	74	3	13	23	33	43
72	73	2	12	22	32	42	52	62
1	11	21	31	41	51	61	71	81
20	30	40	50	60	70	80	9	10
39	49	59	69	79	8	18	19	29
58	68	78	7	17	27	28	38	48
77	6	16	26	36	37	47	57	67

結果3.左高右低，先橫後豎

37	30	23	16	9	74	67	60	53
54	38	31	24	17	1	75	68	61
62	46	39	32	25	18	2	76	69
70	63	47	40	33	26	10	3	77
78	71	55	48	41	34	27	11	4
5	79	72	56	49	42	35	19	12
13	6	80	64	57	50	43	36	20
21	14	7	81	65	58	51	44	28
29	22	15	8	73	66	59	52	45

結果4.左高右低，先豎後橫

5	78	70	62	54	37	29	21	13
22	14	6	79	71	63	46	38	30
39	31	23	15	7	80	72	55	47
56	48	40	32	24	16	8	81	64
73	65	57	49	41	33	25	17	9
18	1	74	66	58	50	42	34	26
35	27	10	2	75	67	59	51	43
52	44	36	19	11	3	76	68	60
69	61	53	45	28	20	12	4	77

再通過鏡像或旋轉，可衍生出更多結果。