久保理論是關於金屬粒子電子性質的理論。它是由久保及其合作者提出的,以後久保和其他研究者進一步發展了這個理論。1986年Halperin對這一理論進行了較全面歸納,並用這一理論對金屬超微粒子的量子尺寸效應進行了深入的分析。
久保理論是針對金屬超微顆粒費米面附近電子能級狀態分布而提出來的,它與通常處理大塊材料費米面附近電子態能級分布的傳統理論不同,有新的特點,這是因為當顆粒尺寸進入納米級時由於量子尺寸效應原大塊金屬的準連續能級產生離散現象。
費米面:k空間占有電子與不占有電子區域的分界面,費米面的能量值為費米能E
 久保理論
久保理論開始,人們把低溫下單個小粒子的費米面附近電子能級看成等間隔的能級。按這一模型計算單個超微粒子的比熱可表示成:
c(T)=kexp(-δ/kT)
式中: δ:能級間隔;k:玻爾茲曼常數; T:絕對溫度。
在高溫下,kT>>δ,溫度與比熱呈線性關係,這與大塊金屬的比熱關係基本一致,然而在低溫下(T→0),KT<<δ,則與大塊金屬完全不同、它們之間為指數關係。
儘管用等能級近似模型推導出低溫下單超微粒子的比熱公式,但實際上無法用實驗證明,這是因為我們只能對超微顆粒的集合體進行實驗。如何從一個超微顆粒的新理論解決理論和實驗相脫離的因難,這方面久保做出了傑出的貢獻。
久保對小顆粒的大集合體的電子能態做了兩點主要假設:
(1)簡併費米液體假設
把超微粒子靠近費米面附近的電子狀態看作是受尺寸限制的簡併電子氣,假設它們的能級為準粒子態的不連續能級,而準粒子之間互動作用可忽略不計。當kT<<δ(相鄰二能級間平均能級間隔)時,這種體系靠近費米面的電子能級分布服從Poisson分布:
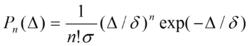 久保理論
久保理論式中:Δ:二能態之間間隔; P(Δ):對應Δ的機率密度; n :二能態間的能級數。
如果Δ為相鄰能級間隔,則n=0。間隔為Δ的二能態的幾率P(Δ)與哈密頓量(Hamiltonian)的變換性質有關。例如,在自旋與軌道互動作用弱和外加磁場小的情況下,電子哈密頓量具有時空反演的不變性,且在Δ比較小的情況下,P(Δ)隨Δ減小而減小。久保的模型優越於等能級間隔模型,比較好地解釋了低溫下超微粒子的物理性能。
(2)超微粒子電中性假設
久保認為,對於一個超微粒子取走或放入一個電子都是十分困難的。他提出了一個著名公式
kT<< W ≈e /d = 1.5×10 k/dK (Å)
式中:W:為從一個超微粒子取出或放入一個電子克服 庫侖力所做的功;
d: 為超微粒直徑;
e: 為電子電荷。
由此式表明隨d值下降,W增加,所以低溫下熱漲落很難改變超微粒子電中性。
在足夠低的溫度下,有人估計當顆粒尺寸為1nm時,W比δ小兩個數量級,根據公式可知kT<<δ,可見1nm的小顆粒在低溫下量子尺寸效應很明顯。 針對低溫下電子能級是離散的,且這種離散對材料熱力學性質起很大作用,例如,超微粒的比熱、磁化率明顯區別於大塊材料,久保及其合作者提出相鄰電子能級間距和顆粒直徑的關係,提出著名的公式:
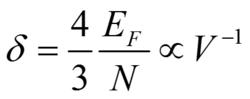 久保理論
久保理論式中: N:為一個超微粒的總導電電子數;
V:為超微粒體積;
E:為費米能級,它可以用下式表示
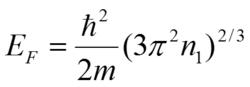 久保理論
久保理論n1 : 電子密度 m : 電子質量
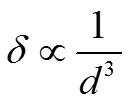 久保理論
久保理論由上式看出,當粒子為球形時, ,即隨粒徑的減小,能級間隔增大。
久保理論提出後,長達約20年之久一直存在爭論,原因在於理論與某些研究者的實驗結果存在不一致之處。例如,1984年Cavicchi等發現,從一個超微金屬粒子取走或放入一個電子克服庫侖力做功(W)的絕對值從0到e /d有一個均勻的分布,而不是久保理論指出的為一常數(e /d)。1986年Halperin經過深入的研究指出,W的變化是由於在實驗過程中電子由金屬粒子向氧化物或其他支撐試樣的基體傳輸量的變化所引起的,因此,他認為實驗結果與久保理論的不一致性不能歸結為久保理論的不正確性,而在於實驗本身。
20世紀70至80年代,超微粒子製備的發展和實驗技術不斷完善,在超微粒物性的研究上取得了一些突破性的進展。例如,用電子自旋共振、磁化率、磁共振和磁弛豫及比熱等測量結果都證實了超微粒子存在量子尺寸效應,這就進一步支持和發展了久保理論。當然,久保理論本身存在許多不足之處,因此,久保理論提出後一些科學工作者對它進行了修正。下節將介紹Denton等人對久保理論的的修正。
