簡介
在算法分析中, 主定理(英語:master theorem)提供了用漸近符號(大O符號)表示許多由分治法得到的遞推關係式的方法。這種方法最初由Jon Bentlery,Dorothea Haken和James B. Saxe在1980年提出,在那裡被描述為解決這種遞推的“天下無敵法”(master method)。此方法經由經典算法教科書Cormen,Leiserson,Rivest和Stein的《算法導論》 (introduction to algorithm) 推廣而為人熟知。
定理
不過,並非所有遞推關係式都可套用主定理。該定理的推廣形式包括Akra-Bazzi定理。
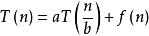 主定理
主定理 主定理
主定理 主定理
主定理 主定理
主定理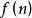 主定理
主定理假設有遞推關係式 ,其中 為問題規模, 為遞推的子問題數量, 為每個子問題的規模(假設每個子問題的規模基本一樣), 為遞推以外進行的計算工作。
a≥1,b>1為常數,f(n) 為函式,T(n) 為非負整數。則有以下結果(分類討論):
 主定理
主定理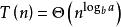 主定理
主定理(1)若 那么
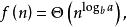 主定理
主定理 主定理
主定理(2)若 那么
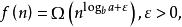 主定理
主定理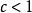 主定理
主定理 主定理
主定理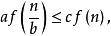 主定理
主定理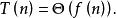 主定理
主定理(3)若 且對於某個常數 和所有充分大的 有 那么
算法分析
在計算機科學中, 算法分析(英語:Analysis of algorithm)是分析執行一個給定算法需要消耗的計算資源數量(例如計算時間,存儲器使用等)的過程。算法的效率或複雜度在理論上表示為一個函式。其定義域是輸入數據的長度(通常考慮任意大的輸入,沒有上界),值域通常是執行步驟數量(時間複雜度)或者存儲器位置數量(空間複雜度)。算法分析是計算複雜度理論的重要組成部分。
理論分析常常利用漸近分析估計一個算法的複雜度,並使用大O符號、大Ω符號和大Θ符號作為標記。舉例,二分查找所需的執行步驟數量與查找列表的長度之對數成正比,記為{\displaystyle O(\log n)},簡稱為“對數時間”。通常使用漸近分析的原因是,同一算法的不同具體實現的效率可能有差別。但是,對於任何給定的算法,所有符合其設計者意圖的實現,它們之間的性能差異應當僅僅是一個係數。
精確分析算法的效率有時也是可行的,但這樣的分析通常需要一些與具體實現相關的假設,稱為計算模型。計算模型可以用抽象機器來定義,比如圖靈機。或者可以假設某些基本操作在單位時間內可完成。
假設二分查找的目標列表總共有 n 個元素。如果我們假設單次查找可以在一個時間單位內完成,那么至多只需要{\displaystyle \log n+1}單位的時間就可以得到結果。這樣的分析在有些場合非常重要。
算法分析在實際工作中是非常重要的,因為使用低效率的算法會顯著降低系統性能。在對運行時間要求極高的場合,耗時太長的算法得到的結果可能是過期或者無用的。低效率算法也會大量消耗計算資源。
分治法
在計算機科學中, 分治法是建基於多項分支遞歸的一種很重要的算法範式。字面上的解釋是“分而治之”,就是把一個複雜的問題分成兩個或更多的相同或相似的子問題,直到最後子問題可以簡單的直接求解,原問題的解即子問題的解的合併。
這個技巧是很多高效算法的基礎,如排序算法(快速排序、歸併排序)、傅立葉變換(快速傅立葉變換)。
另一方面,理解及設計分治法算法的能力需要一定時間去掌握。正如以歸納法去證明一個理論,為了使遞歸能夠推行,很多時候需要用一個較為概括或複雜的問題去取代原有問題。而且並沒有一個系統性的方法去適當地概括問題。
分治法這個名稱有時亦會用於將問題簡化為只有一個細問題的算法,例如用於在已排序的列中查找其中一項的折半搜尋算法(或是在數值分析中類似的勘根算法)。這些算法比一般的分治算法更能有效地運行。其中,假如算法使用尾部遞歸的話,便能轉換成簡單的循環。但在這廣義之下,所有使用遞歸或循環的算法均被視作“分治算法”。因此,有些作者考慮“分治法”這個名稱應只用於每個有最少兩個子問題的算法。而只有一個子問題的曾被建議使用 減治法這個名稱。
