基本介紹
中間態(intermediate state)是退磁因子D不為零的第一類超導體處於外磁場中時,由於超導體的磁化使磁場分布畸變,結果產生不均勻的表面場,如圖所示。外場增加時,超導體表面某些區域首先達到臨界磁場轉變為正常態,而其它區域仍為超導態。這種超導態與正常態同時存在的狀態稱為 中間態。
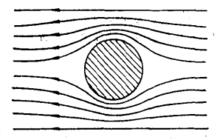 圖1 超導體附近的磁場分布
圖1 超導體附近的磁場分布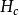 中間態
中間態蘭道首先分析了無限超導平板在橫場中的情況,認為這時超導體將分成許多交替出現的超導相和正常相超導球附近的磁場分布薄層,稱為 層狀結構模型。外場增加時正常相的體積增加,外場達到 時全部轉變為正常相。蘭道認為,正常相薄層在超導體表面要變寬並分裂為許多更薄的層,稱為 分支層狀結構。後來的實驗證明了層狀結構模型,但只在很少的情況下才能觀察到類似於蘭道的分支結構。
第一類超導體的中間態與第二類超導體的混合態,都是正常態與超導態之間的過渡階段,但它們的內部結構不同。在退磁因子不為零的第二類超導中,邁斯納態與混合態共存的狀態也稱為中間態 。
中間態結構
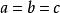 中間態
中間態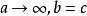 中間態
中間態 中間態
中間態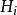 中間態
中間態為了便於處理問題,以橢球作為研究對象。對於橢球,當 時,橢球可以化為球:當 時橢球可以化為圓柱體。假設超導橢球體在外加磁場 中被磁化,橢球內部磁介質的磁場強度為 ,則有
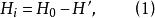 中間態
中間態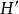 中間態
中間態 中間態
中間態式中, 稱為退磁場,退磁場與橢球內磁化強度 成正比
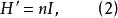 中間態
中間態式中的比例係數n是退磁因子,表1列出了一些幾何結構的退磁因子 。
| 超導體的形狀 | 外磁場取向 |  中間態 中間態 | 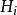 中間態 中間態 |
| 球 | 任意方向 |  中間態 中間態 | 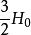 中間態 中間態 |
| 圓柱體 | 與圓柱軸平行 | 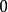 中間態 中間態 |  中間態 中間態 |
| 圓柱體 | 與圓柱軸垂直 |  中間態 中間態 | 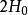 中間態 中間態 |
| 無限大平板 | 與平板平行 | 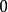 中間態 中間態 |  中間態 中間態 |
| 無限大平板 | 與平板垂直 |  中間態 中間態 |  中間態 中間態 |
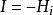 中間態
中間態對於超導體,在超導態 時,如果把式(2)代入式(1),可以得到
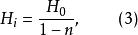 中間態
中間態從而得到
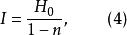 中間態
中間態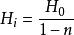 中間態
中間態當橢球處於超導態時,其內部磁場強度可以寫為 。如果設超導
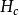 中間態
中間態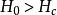 中間態
中間態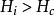 中間態
中間態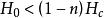 中間態
中間態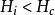 中間態
中間態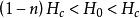 中間態
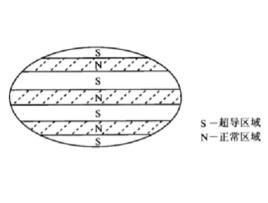
中間態體的臨界磁場為 ,當 ,那么 ,橢球處於正常態。當 時, ,橢球處於超導態。然而當 時,稱為 超 導體處於中間態。所謂中間態是指超導橢球界於正常態和超導態中間的一種狀態,即整個超導橢球分割成正常層和超導層相互交替的結構( 見圖2)。
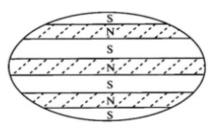 圖2 中間態的分層結構
圖2 中間態的分層結構S——超導區域;N——正常區域。
為了便於討論中間態,引入平均磁感應強度
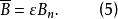 中間態
中間態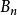 中間態
中間態 中間態
中間態式中, 為正常區內局域磁感應強度; 是正常層部分所在的分數。
因此
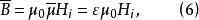 中間態
中間態由
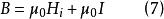 中間態
中間態得
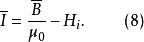 中間態
中間態由式(1)和式(2),得到
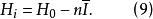 中間態
中間態由式(6)和式(8),得到
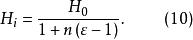 中間態
中間態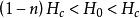 中間態
中間態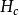 中間態
中間態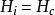 中間態
中間態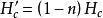 中間態
中間態注意: ,超導體進人中間態劈裂成超導層和正常層結構,中間態結構中,在超導層和正常層共存的邊界上磁場強度的大小等於 ,利用 和 ,由式(10)可以得到
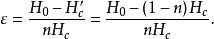 中間態
中間態將此方程代人式(6),得到
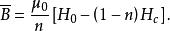 中間態
中間態將上式代人(8),得到
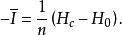 中間態
中間態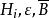 中間態
中間態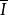 中間態
中間態 中間態
中間態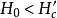 中間態
中間態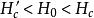 中間態
中間態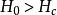 中間態
中間態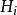 中間態
中間態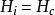 中間態
中間態 中間態
中間態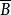 中間態
中間態 中間態
中間態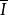 中間態
中間態 中間態
中間態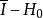 中間態
中間態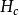 中間態
中間態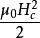 中間態
中間態表1給出了中間態 和 外加磁場 的關係。其中給出了外磁場 時處於邁斯納態, 處於中間態以及 處於正常態下這些參量的關係曲線。在中間態 保持不變, ; 和 在中間態隨著外磁場 的增加線性增加; 隨著外磁場 的增加線性降低。通常 曲線稱為 磁化曲線。應當指出,不管n值如何,當外磁場從零增加到 時,磁化曲線的面積不變,總等於 。
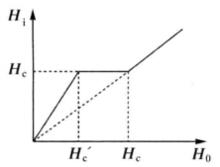 (a) (a) | 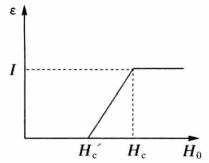 (b) (b) |
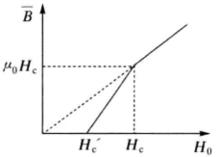 (c) (c) | 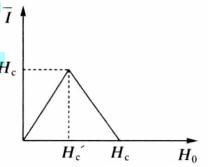 (d) (d) |
超導體
超導體特性
超導體具有完全導電性和完全抗磁性。這些有益的特性使超導在國民經濟各方面具有廣闊的前景。
完全導電性指進入超導態時沒有電阻,超導電流將持續流動。進入超導態的超導體中有電流而沒有電阻,說明超導體是等電位的,超導體內沒有電場。如在室溫下將超導體放到磁場中,冷卻到臨界溫度以下使其進入超導態。這時如果將磁場移開,超導體中產生的感生電流由於沒有電阻而長期存在,成為無衰減的電流。
超導態的另一個特性是它存在完全抗磁性。處於超導態的材料不管處於何種狀態,磁感應強度均為0,稱為 邁斯納效應。這說明處於超導態的超導體是抗磁體。此時超導體具有禁止磁場和排除磁通的功能。如圖3所示,超導體做成圓球並使之處於正常態時,磁通通過導體;當球處於超導態時,磁通被排斥在外,內部磁場為0。
 中間態
中間態超導體處於超導態需要滿足三個條件。①低於臨界轉變溫度。超導體必須冷卻到某一臨界溫度以下才能保持其電導性。顯然,臨界轉變溫度越高則實用價值越高。②低於臨界磁場強度,施加給超導體的磁場必須小於某一臨界磁場才能保持超導體的超導性能。③低於臨界電流密度。超導體的電流密度必須小於某一臨界
電流密度才能保持超導體的超導性。以上三個條件是彼此關聯的,只有處於三個臨界約束條件包圍的三維空間中超導體才具有超導電性 。
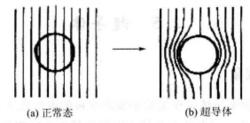 圖3 邁斯納效應
圖3 邁斯納效應超導體的分類
按超導體的磁化特性可以分為兩類。 第一類超導體和 第二類超導體。第一類超導體的特徵為正常態直接過渡到超導態,無中間態,並且具有完全抗磁性。該超導體熔點較低、質地較軟,也稱 軟超導體,包括一些在常溫下具有良好導電性的純金屬,如鋁、鎵、鎘、錫、銦等。第一類超導體由於臨界電流密度和臨界磁場較低,因而實用價值不大。
第二類超導體與第一類超導體主要區別在於:由正常態轉變為超導態時存在中間態,混合態中有磁通線存在,具有比第一類超導體更高的臨界轉變溫度、更大的臨界電流密度和更高的臨界磁場強度。第二類超導材料也因此具有重大的實用價值 。