定義
三角形中,連結一個頂點和它所對邊的中點的連線段叫做三角形的中線。
中線也是線段 ,一個三角形有3條中線。
性質
(1)任意三角形的三條中線把三角形分成面積相等的六個部分。中線都把三角形分成面積相等的兩個部分。除此之外,任何其他通過中點的直線都不把三角形分成面積相等的兩個部分。
![中線[幾何概念]](/img/3/1c3/wZwpmL1gzM2QDO0UTM0kDN1UTM1QDN5MjM5ADMwAjMwUzL1EzL3AzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 中線[幾何概念]
中線[幾何概念]![中線[幾何概念]](/img/c/d80/wZwpmL1YTNwITNxMDO0YzM1UTM1QDN5MjM5ADMwAjMwUzLzgzLyAzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 中線[幾何概念]
中線[幾何概念]![中線[幾何概念]](/img/1/bc7/wZwpmL2MDO3gDNyMDM0kDN1UTM1QDN5MjM5ADMwAjMwUzLzAzLyIzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 中線[幾何概念]
中線[幾何概念]![中線[幾何概念]](/img/8/6da/wZwpmL4cDMzgjM5QTOzkDN1UTM1QDN5MjM5ADMwAjMwUzL0kzLxUzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 中線[幾何概念]
中線[幾何概念](2)在ABC中,連線角A的中線記為,連線角B的中線記為,連線角C的中線記為,它們長度的公式為:
![中線[幾何概念]](/img/8/e99/wZwpmLzADO5MTMwgDM0kDN1UTM1QDN5MjM5ADMwAjMwUzL4AzLyMzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 中線[幾何概念]
中線[幾何概念]![中線[幾何概念]](/img/8/cda/wZwpmLwIDN0IzNykDOzkDN1UTM1QDN5MjM5ADMwAjMwUzL5gzL0MzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 中線[幾何概念]
中線[幾何概念]![中線[幾何概念]](/img/2/2b0/wZwpmL4EzM4YDO4gDOzkDN1UTM1QDN5MjM5ADMwAjMwUzL4gzL2gzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg) 中線[幾何概念]
中線[幾何概念](3)三角形中中線的交點為重心,重心分中線為2:1(頂點到重心:重心到對邊中點)。
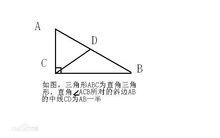 圖中線段CD即為三角形ABC的其中一條中線。
圖中線段CD即為三角形ABC的其中一條中線。(4)在一個直角三角形中,直角所對應的邊上的中線為斜邊的一半。
方法
倍長中線法:倍長中線的意思是,延長底邊的中線,使所延長部分與中線相等,然後往往需要連線相應的頂點,則對應角對應邊都對應相等。
此法常用於構造全等三角形,利用中線的性質進而證明對應邊之間的關係。
示例
已知(如圖)AE是ABD中BD邊上的中線,AB=CD,∠BAD=∠ADB。
![中線[幾何概念]](/img/0/da7/wZwpmL2EzM2QjM5QDM0kDN1UTM1QDN5MjM5ADMwAjMwUzL0AzL0MzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 中線[幾何概念]
中線[幾何概念]求證:AC=2AE。
分析:這也是一道巧用中線的證明題,原題要求我們證出AC=2AE。而AE在圖形中恰好是一個三角形的中線,我們知道要證兩條線段相等,只要證兩條線段所在的兩個三角形全等就可以。
而圖形中沒有2AE這條線段,這樣我們就必須構造出一個全新的三角形,使其中一邊的長為2AE,延長AE至點P,使AE=EP(AP=2AE),連結BP,從而得到一個新的三角形△ABP。進而證得△ABP和三角形ADC全等,從而證AC=AP,即AC=2AE。
![中線[幾何概念] 中線[幾何概念]](/img/2/f2f/nBnauM3X1IjMwMDMygDMxADO1UTM1QDN5MjM5ADMwAjMwUzL4AzL4MzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg)
