定義
如果粒子受某種作用的限制，因而在空間某區域內發現該粒子的機率遠大於其他區域，則此區域常可看做一個勢阱（例：電子在金屬固體中運動；質子、中子被束縛在原子核中。）。為簡化問題的討論，往往假定粒子在外力場中的勢函式為
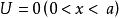一維無限深勢阱
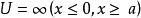一維無限深勢阱該理想化模型稱作一維無限深勢阱。
實際模型
在金屬中的自由電子不會自發地逃出金屬，它們在各晶格結點（正離子）形成的“周期場”中運動。進一步簡化這個模型，可以粗略地認為粒子被“無限高”的勢能壁束縛在金屬之中，由此而抽象出粒子在無限深勢阱中運動。為簡單起見，設勢阱是一維的，這是量子力學中最簡單的例子。自由電子在一塊金屬中的運動相當於在勢阱中的運動。在阱內，由於勢能為零，粒子受到的總的力為零，其運動是自由的。在邊界上x=0或x=a處，由於勢能突然增加到無限大，粒子受到無限大指向阱內的力。因此，粒子的位置不可能到達0<x<a的範圍以外。
波函式
一維無限深勢阱
一維無限深勢阱設粒子有效質量為 ，粒子運動的波函式為 。
在阱內（0<x<a），體系的定態薛丁格方程為
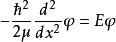一維無限深勢阱①
在阱外（x>a,x<0），體系的定態薛丁格方程為
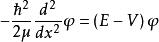一維無限深勢阱②
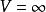一維無限深勢阱
一維無限深勢阱由於阱外 ，阱外波函式 。
由波函式的統計詮釋可知，在x=0和x=a兩點波函式連續，因此要求阱內波函式滿足
φ(0)=0, φ(a)=0 ③
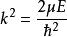一維無限深勢阱①式中，令 ，方程的解具有以下形式
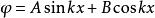一維無限深勢阱④
將③代入④，得B=0，Asinka=0。由於A=0時φ=0，波函式無意義，因此sinka=0，解出
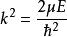一維無限深勢阱ka=nπ，將該結果代入④以及 ，可得出粒子能級以及波函式。
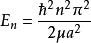一維無限深勢阱
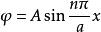一維無限深勢阱
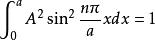一維無限深勢阱
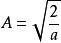一維無限深勢阱
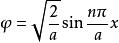一維無限深勢阱將波函式歸一化， ，因此 ，波函式
