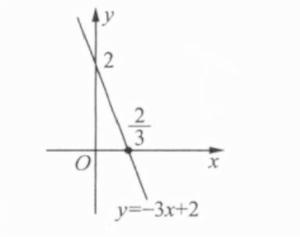
基本概念
在實際問題中,如果所含兩個變數之間的依存關係是線性的,則可通過建構一次函式加以解決。形如y=ax+b(a≠0)的函式稱為 一元一次函式 。
一元一次函式的性質
對於一元一次函式要注意如下幾點:
(1)一元一次函式y=ax+b(a≠0)中的x取值範圍(定義域)是全體實數。如果人為限定x的取值範圍,那么定義域則與限定的取值範圍一致。
(2)一元一次函式y=ax+b(a≠0)是增還是減根據a的正負性來判斷。若a>0,則函式為增函式;若a<0,則函式為減函式。
(3)一元一次函式y=ax+b(a≠0)的函式圖像所體現出來的特徵:
在a>0情況下:
若b>0,則函式通過一、二、三象限;
若b<0函式通過一、三、四象限。
在a<0情況下:
若b>0,則函式通過一、二、四象限;
若b<0函式通過二、三、四象限。
(4)當y=ax+b(a≠0)中的b=0時,則函式必通過原點(0,0),如圖1和圖2所示 。
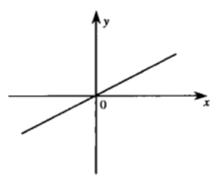 圖1 圖1 | 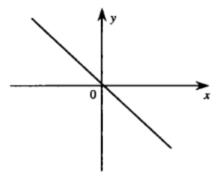 圖2 圖2 |
5.一元一次函式y=ax+b(a≠0)是一元線性函式。線性函式(linear function)是一類重要的有理函式,指一個或多個自變數的齊次或非齊次的一次整式所表示的函式。分兩種形式:
1.一元線性函式。通常指一次函式y=kx+b(k,b均為常數,k≠0),線性函式的基本性質是:函式值的增量與自變數的增量成正比例,在直角坐標平面中,線性函式的圖象是一條直線。
2.多元線性函式。形如f(x,x,…,x)=ax+ax+…+ax+a(其中a,a,…,a,a是常數,且a,…,a不全為零)的函式稱為n元線性函式,又稱n元一次函式.n元線性函式的定義域是n個實(或復)變數x,x,…,x的整個n維空間.當a=0時,上述形式的線性函式稱為齊次線性函式或線性型。如果變數x,x,…,x與係數a,a,…,a,a都是實數,那么n維線性函式在變數x,x,…,x,y的(n+1)維空間中的圖象是n維超平面y=ax+ax+…ax+a。線性齊次函式的同義語是線性型 。
例題解析
【例1】一次函式y=ax+b(a≠0),如果a>0,b>0,則函式必過( )象限
A.二、三、四
B.一、三、四
C.一、二、四
D.一、二、三
E.無法判斷
答:選D。
圖像大致如圖3,若a<0,b>0則選C,圖像大致如圖4。
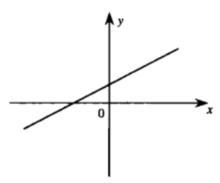 圖3 圖3 | 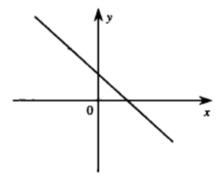 圖4 圖4 |