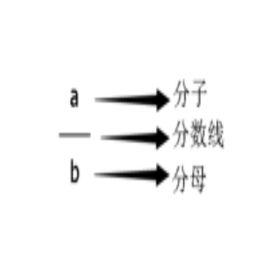
分數
分數(來自拉丁語,“破碎”)代表整體的一部分,或更一般地,任何數量相等的部分。 當在日常英語中說話時,分數描述了一定大小的部分,例如半數,八分之五,四分之三。 分子和分母也用於不常見的分數,包括複合分數,複數分數和混合數字。
分數表示一個數是另一個數的幾分之幾,或一個事件與所有事件的比例。把單位“1”平均分成若干份,表示這樣的一份或幾份的數叫分數。分子在上,分母在下。
最早的分數是整數倒數:代表二分之一的古代符號,三分之一,四分之一,等等。埃及人使用埃及分數c。 1000 bc。大約4000年前,埃及人用分數略有不同的方法分開。他們使用最低公倍數與單位分數。他們的方法給出了與現代方法相同的答案。埃及人對於Akhmim木片和二代數學紙莎草的問題也有不同的表示法。
簡介
國小定義:被除數除以除數等於除數分之被除數,即:除法里的除數即相當於分數中的分母。
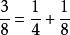 分母
分母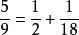 分母
分母古埃及人曾經考慮關於如下問題:如何將一個分數寫成形如1/n的分數之和?即寫成那些分子是1,分母是正整數的分數之和, 且要求分母互不相同,如,等。
(說明:現代數學中,此類分數稱為“單位分數”,其定義為——分子是1,分母是等於或大於2的自然數的分數叫做單位分數,記為1/n。)
這一問題可以歸結為某類連分數的構造問題, 進一步和著名的戴德金互反律聯繫起來,因此它也和Hirzebruch奇點有著密切關係。
特點
1、分母表示一個總體的數值,分子表示占用分母比率。
2、分式中,將寫在分數線下面的數或代數式稱為分母,它的意義是表示把單位1平均分成若干份。
3、分母是已知數的分數叫整式,分母是未知數的分數叫分式。
注意事項
1、分母可以為除了0以外的一切數,即分母不等於0。
在任意分數中,若分母等於0,此分數無意義。
2、在一個繁分數里,最長的分數線叫做繁分數的主分數線,主分數線上下不管有多少個數或運算,都把它們分別看作是繁分數的分子和分母。
分母有理化
分母有理化(fēn mǔ yǒu lǐ huà)(Rationalize the denominator),又稱"有理化分母",指的是在二次根式中分母原為無理數,而將該分母化為有理數的過程,也就是將分母中的根號化去。
下面介紹兩種分母有理化的常規方法,基本思路是把分子和分母都乘以同一個適當的代數式,使分母不含根號。
分母是一個單項式
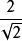 分母
分母例如二次根式,下面將之分母有理化:
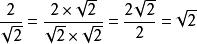 分母
分母 分母
分母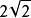 分母
分母 分母
分母 分母
分母分子分母同時乘以,分母變為2,分子變為,約分後,分數值為。在這裡我們想辦法把化為有理數,只要變為它的平方即可。
分母是一個多項式
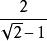 分母
分母再舉一個分母是多項式的例子,如,下面將之分母有理化:
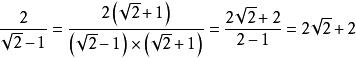 分母
分母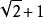 分母
分母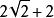 分母
分母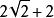 分母
分母思路仍然是將分子分母同乘相同數。這裡使用平方差公式,同時乘上,分子變為,分數值為,再約分即可。也就是說,為了有理化多項式的分母,原來分母是減號,我們乘上一個數字相同但用加號連線的式子,再用平方差公式。
此方法可套用到根式大小比較中去。
去分母
去分母是指等式兩邊同時乘以分母的最低公倍數。
等式兩邊同時乘以分母的最低公倍數。
對於方程: 1)先找出所有分母的最簡公分母 ;2)在方程兩邊同乘以最低公倍數。
對於不等式:不能隨意消去含有未知數的分母。
對於代數式:只能通過約分的方式,才能消去分母。
示例
•3÷8寫成分數是3/8 ,其中“8”叫分母。
•c÷(a+b)寫成分數是c/(a+b),其中“a+b”叫分母。
•2/5,a/b,c/(a+b) 等數或式里的“5”,“b”,"a+b",都叫分母。