模型定義
一.VaR模型基本思想
VaR按字面的解釋就是“處於風險狀態的價值”,即在一定置信水平和一定持有期內,某一金融工具或其組合在未來資產價格波動下所面臨的最大損失額。JP.Morgan定義為:VaR是在既定頭寸被沖銷(be neutraliged)或重估前可能發生的市場價值最大損失的估計值;而Jorion則把VaR定義為:“給定置信區間的一個持有期內的最壞的預期損失”。
二.VaR基本模型
根據Jorion(1996),VaR可定義為:
VaR=E(ω)-ω* ①
式中E(ω)為資產組合的預期價值;ω為資產組合的期末價值;ω*為置信水平α下投資組合的最低期末價值。
又設ω=ω0(1+R) ②
式中ω0為持有期初資產組合價值,R為設定持有期內(通常一年)資產組合的收益率。
ω*=ω0(1+R*) ③
R*為資產組合在置信水平α下的最低收益率。
根據數學期望值的基本性質,將②、③式代入①式,有
VaR=E[ω0(1+R)]-ω0(1+R*)
=Eω0+Eω0(R)-ω0-ω0R*
=ω0+ω0E(R)-ω0-ω0R*
=ω0E(R)-ω0R*
=ω0[E(R)-R*]
∴VaR=ω0[E(R)-R*] ④
上式公式中④即為該資產組合的VaR值,根據公式④,如果能求出置信水平α下的R*,即可求出該資產組合的VaR值。
三.VaR模型的假設條件
VaR模型通常假設如下:
⒈市場有效性假設;
⒉市場波動是隨機的,不存在自相關。
一般來說,利用數學模型定量分析社會經濟現象,都必須遵循其假設條件,特別是對於我國金融業來說,由於市場尚需規範,政府干預行為較為嚴重,不能完全滿足強有效性和市場波動的隨機性,在利用VaR模型時,只能近似地正態處理。
計算方法
從前面①、④兩式可看出,計算VAR相當於計算E(ω)和ω*或者E(R)和R*的數值。從目前來看,主要採用三種方法計算VaR值。
⒈歷史模擬法(historical simulation method)
⒉方差—協方差法
⒊蒙特卡羅模擬法(Monte Carlosimulation)
一.歷史模擬法
“歷史模擬法”是藉助於計算過去一段時間內的資產組合風險收益的頻度分布,通過找到歷史上一段時間內的平均收益,以及在既定置信水平α下的最低收益率,計算資產組合的VaR值。
“歷史模擬法”假定收益隨時間獨立同分布,以收益的歷史數據樣本的直方圖作為對收益真實分布的估計,分布形式完全由數據決定,不會丟失和扭曲信息,然後用歷史數據樣本直方圖的P—分位數據作為對收益分布的P—分位數—波動的估計。
一般地,在頻度分布圖中(圖1,見例1)橫軸衡量某機構某日收入的大小,縱軸衡量一年內出現相應收入組的天數,以此反映該機構過去一年內資產組合收益的頻度分布。
首先,計算平均每日收入E(ω)
其次,確定ω*的大小,相當於圖中左端每日收入為負數的區間內,給定置信水平 α,尋找和確定相應最低的每日收益值。
設定信水平為α,由於觀測日為T,則意味差在圖的左端讓出
t=T×α,即可得到α機率水平下的最低值ω*。由此可得:
VaR=E(ω)-ω*
二.方差—協方差法
“方差—協方差”法同樣是運用歷史資料,計算資產組合的VaR值。其基本思路為:
首先,利用歷史數據計算資產組合的收益的方差、標準差、協方差;
其次,假定資產組合收益是常態分配,可求出在一定置信水平下,反映了分布偏離均值程度的臨界值;
第三,建立與風險損失的聯繫,推導VaR值。
設某一資產組合在單位時間內的均值為μ,數準差為σ,R*~μ(μ、σ),又設α為置信水平α下的臨界值,根據常態分配的性質,在α機率水平下,可能發生的偏離均值的最大距離為μ-ασ,
即R*=μ-ασ。
∵E(R)=μ
根據VaR=ω0[E(R)-R*] 有
VaR=ω0[μ-(μ-ασ)]=ω0ασ
假設持有期為 △t,則均值和數準差分別為μ△t和 ,這時上式則變為:
VaR=ω0·α·
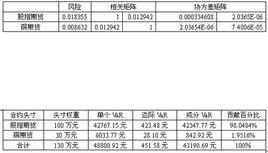
因此,我們只要能計算出某種組合的標準差σ,則可求出其VaR的值,一般情況下,某種組合的數準差σ可通過如下公式來計算
其中,n為資產組合的金融工具種類,Pi為第i種金融工具的市場價值,σi第i種金融工具的標準差,σij為金融工具i、j的相關係數。
除了歷史模擬法和方差—協方差外,對於計算資產組合的VaR的方法還有更為複雜的“蒙特卡羅模擬法”。它是基於歷史數據和既定分布假定的參數特徵,藉助隨機產生的方法模擬出大量的資產組合收益的數值,再計算VaR值。
根據古德哈特等人研究,計算VaR值三種方法的基本步驟及特徵如下表。
.
風險估價技術比較
分類
步驟HSMVaR—Cov Monte—Carlo
⒈確認頭寸 找到受市場風險影響的各種金融工具的全部頭寸
⒉確認風險因素 確認影響資產組合中金融工具的各種風險因素
⒊獲得持有期內風險因素的收益分布 計算過去年份里的歷史上的頻度分布 計算過去年份里風險因素的標準差和相關係數 假定特定的參數分布或從歷史資料中按自助法隨機產生
⒋將風險因素的收益與金融工具頭寸相聯繫 將頭寸的盯住市場價值(mark to market value)表示為風險因素的函式 按照風險因素分解頭寸(risk mapping) 將頭寸的盯住市場價值(mark to market value)表示為風險因素的函式
⒌計算資產組合的可變性 利用從步驟3和步驟4得到的結果模擬資產組合收益的頻度分布 假定風險因素是呈常態分配,計算資產組合的標準差 利用從步驟3和步驟4得到的結果模擬資產組合收益的頻度分布
⒍給定置信區間推導VAR
排列資產組合順序,選擇剛好在1%或5%機率下剛≥1的那一損失
用2.33(1%)或1.65(5%)乘以資產組合標準差 排列資產組合順序,選擇剛好在1%或5%機率下剛≥1的那一損失
VaR模型在金融風險管理中的套用
VaR模型在金融風險管理中的套用越來越廣泛,特別是隨著VaR模型的不斷改進,不但套用於金融機構的市場風險、使用風險的定量研究,而且VaR模型正與線性規劃模型(LPM)和非線性規劃模型(ULPM)等規劃模型論,有機地結合起來,確定金融機構市場風險等的最佳定量分析法,以利於金融機構對於潛在風險控制進行最優決策。
對於VaR在國外的套用,正如文中引言指出,巴塞爾委員會要求有條件的銀行將VaR值結合銀行內部模型,計算適應市場風險要求的資本數額;G20建議用VaR來衡量衍生工具的市場風險,並且認為是市場風險測量和控制的最佳方法;SEC也要求美國公司採用VaR模型作為三種可行的披露其衍生交易活動信息的方法之一。這表明不但金融機構內部越來越多地採用VaR作為評判金融機構本身的金融風險,同時,越來越多的督管機構也用VaR方法作為評判金融機構風險大小的方法。
我國對VaR模型的引介始於近年,具有較多的研究成果,但VaR模型的套用現在確處於起步階段,各金融機構已經充分認識到VaR的優點,正在研究適合於自身經營特點的VaR模型。