定義
參見：子式和餘子式、余因子矩陣及轉置矩陣。
設 R是一個交換環， A是一個以 R中元素為係數的 n× n 的矩陣。 A的伴隨矩陣可按如下步驟定義：
•定義：A關於第i 行第j 列的餘子式（記作M）是去掉A的第i行第j列之後得到的(n − 1)×(n − 1)矩陣的行列式。
•定義：A關於第i 行第j 列的代數餘子式是：
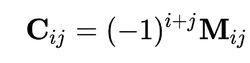代數餘子式•定義：A的餘子矩陣是一個n×n的矩陣C，使得其第i 行第j 列的元素是A關於第i 行第j 列的代數餘子式。
引入以上的概念後，可以定義：矩陣 A的 伴隨矩陣是 A的餘子矩陣的 轉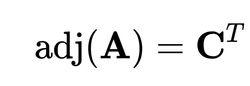置矩陣：
轉置矩陣也就是說， A的 伴隨矩陣是一個 n× n的矩陣（記作adj( A)），使得其第 i 行第 j 列的元素是 A關於第 j 行第 i 列的 代數餘子式：
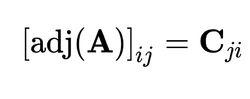代數餘子式-2例子
2x2矩陣
一個2x2矩陣
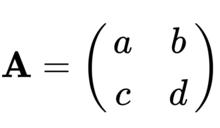1的伴隨矩陣是
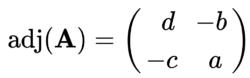23x3矩陣
對於 3x3的矩陣，情況稍微複雜一點：
3其伴隨矩陣是：
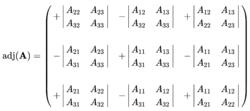4其中
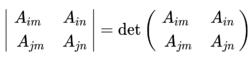5要注意伴隨矩陣是餘子矩陣的轉置，第 3行第 2列的係數應該是 A關於第 2行第 3列的代數餘子式。
具體情況
對於數值矩陣，例如求矩陣
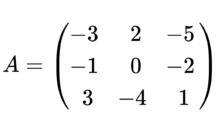6的伴隨矩陣adj( A)，只需將數值代入上節得到的表達式中。
即
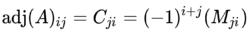8其中 M為刪掉矩陣 A的第 i 橫列與第 j 縱行後得到的行列式， C為矩陣 A的余因子。
例如adj( A) 中 第3列第2行的元素為
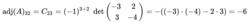10依照其順序一一計算，便可得到計算後的結果是：
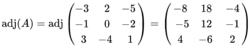11套用
作為拉普拉斯公式的推論，關於 n× n 矩陣 A的行列式，有：
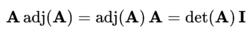12(*)
其中 I是 n階的單位矩陣。事實上， A adj( A)的第 i行第 i列的係數是
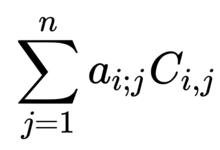13。根據拉普拉斯公式，等於 A的行列式。
如果 i ≠ j，那么 A adj( A)的第 i行第 j列的係數是
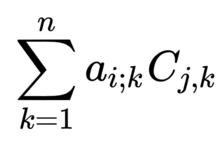14。拉普拉斯公式說明這個和等於0（實際上相當於把 A的第 j行元素換成第 i行元素後求行列式。由於有兩行相同，行列式為0）。
由這個公式可以推出一個重要結論：交換環 R上的矩陣 A可逆若且唯若其行列式在環 R中可逆。
這是因為如果 A可逆，那么
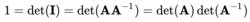15如果det( A)是環中的可逆元那么公式(*)表明
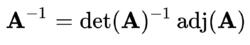16性質
對n×n的矩陣 A和 B，有：
1.adj( Ⅰ)= Ⅰ
2.adj( AB)=adj( B)adj( A)
3.adj( A)=adj( A)
4.det(adj( A))=det( A)
5.
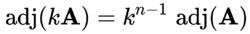176.當n>2時，
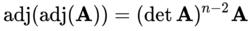187.如果 A可逆，那么
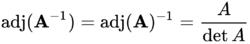198.如果 A是對稱矩陣，那么其伴隨矩陣也是對稱矩陣；如果 A是反對稱矩陣，那么當 n為偶數時， A的伴隨矩陣也是反對稱矩陣， n為奇數時則是對稱矩陣。
9.如果 A是（半）正定矩陣，那么其伴隨矩陣也是（半）正定矩陣。
10.如果矩陣 A和 B相似，那么adj( A)和adj( B)也相似。
11.如果n>2，那么非零矩陣 A是正交矩陣若且唯若adj( A)=± A
伴隨矩陣的秩
當矩陣 A可逆時，它的伴隨矩陣也可逆，因此兩者的秩一樣，都是 n。當矩陣 A不可逆時， A的伴隨矩陣的秩通常並不與 A相同。當 A的秩為 n-1時，其伴隨矩陣的秩為1，當 A的秩小於 n-1時，其伴隨矩陣為零矩陣。
伴隨矩陣的特徵值
設矩陣 A在復域中的特徵值為 λ,λ...λ（即為特徵多項式的 n個根），則 A的伴隨矩陣的特徵值為
λλ...λ，λλ...λ，...，λλ...λ。
伴隨矩陣和特徵多項式
設 p( t) = det( A − tI)為 A的特徵多項式，定義
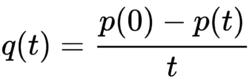20，那么：
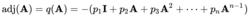21其中是 p( t)的各項係數：
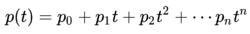22伴隨矩陣也出現在行列式的導數形式中。
參見
- 逆矩陣
- 可逆元
- 餘子矩陣
- 行列式
