術語解釋
總諧波失真一般說來,1000Hz頻率處的總諧波失真最小,因此不少產品均以該頻率的失真作為它的指標。但總諧波失真與頻率有關,必須在20-2O000Hz的全音頻範圍內測出。 總諧波失真表明功放工作時,由於電路不可避免的振盪或其他諧振產生的二次,三次諧波與實際輸入信號疊加,在端輸出的信號就不單純是與輸入信號完全相同的成分,而是包括了諧波成分的信號,這些多餘出來的諧波成分與實際輸入信號的對比,用百分比來表示就稱為總諧波失真。一般來說,總諧波失真在1000赫茲
附近最小,所以大部分功放表明總諧波失真是用1000赫茲信號做測試,但有些更嚴格的廠家也提供20-20000赫茲範圍內的總諧波失真數據。總諧波失真在1%以下,一般耳朵分辨不出來,超過10%就可以明顯聽出失真的成分。這個總諧波失真的數值越小,音色就更加純淨。一般產品的總諧波失真都小於1%@1kHz,但這個數值越小,表明產品的品質越高。計算公式
關於THD的計算公式,不同標準的定義略有不同。公式一
《GBT--17626.7-2008電磁兼容試驗和測量技術供電系統及所連設備諧波、諧間波的測量和測量儀器導則》中,對THD的定義如下:
符號G表示諧波分量的有效值,它將按要求在表示電流時被I代替,在表示電壓時被U代替,H的值在與限制有關的每一個標準中給出。按照上述定義,THD不包含間諧波,並且,有一固定的諧波上限。 公式二
《GB/T12668.2-2002調速電氣傳動系統一般要求低壓交流變頻電氣傳動系統額定值的規定》對THD定義如下:
上式中,Q為總有效值,Q1為基波有效值,可代表電壓或電流,按照上述定義,THD包含間諧波和直流分量。
解析
原因
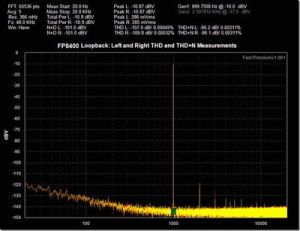 總諧波失真
總諧波失真諧波失真是指音箱在工作過程中,由於會產生諧振現象而導致音箱重放總諧波失真聲音時出現失真。儘管音箱中只有基頻信號才是聲音的原始信號,但由於不可避免地會出現諧振現象(在原始聲波的基礎上生成二次、三次甚至多次諧波),這樣在聲音信號中不再只有基頻信號,而是還包括由諧波及其倍頻成分,這些倍頻信號將導致音箱放音時產生失真。對於普通音箱允許一定諧波信號成分存在,但必須是以對聲音基頻信號輸出不產生大的影響為前提條件。
而總諧波失真是指用信號源輸入時,輸出信號(諧波及其倍頻成分)比輸入信號多出的額外諧波成分,通常用百分數來表示。一般說來,1000Hz頻率處的總諧波失真最小,因此不少產品均以該頻率的失真作為它的指標。所以測試總諧波失真時,是發出1000Hz的聲音來檢測,這一個值越小越好。
備註
一些產品說明書的總諧波失真表示為THD<0.5%,1W,這樣看來總諧波失真較小,但只是在輸出功率為1W的總諧波失真,這與標準要求的測量條件下得到的總諧波失真是不同的。因此,評價MP3的總諧波失真指標時應註明是在什麼條件下測得的。
THD(totalharmonicdistortion,總諧波失真):是聲音設備產生的(通常是不受歡迎的)諧波的水平。一般來說,高質量設備的THD值很低(低於0.002%),但也有例外。很多電子管設備的THD非常高,但電晶體設備必須具有較低的THD,因為它們多餘的諧波會使聲音聽起來很不舒服。
分類
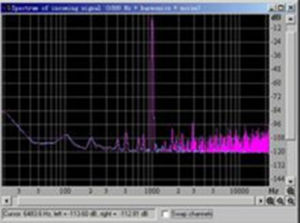 總諧波失真
總諧波失真(l)互調失真(IMD):將互調失真儀輸出的125Hz與lkHz的簡諧信號合成波,按4:1的幅值輸入到被測量的放大器中,從額定負載上測出互調失真係數。
波失真最小,因此不少產品均以該頻率的失真作為它的指標。但總諧波失真與頻率有關,因此美國聯邦貿易委員會於1974年規定,總諧波失真必須在20~20000Hz的全音頻範圍內測出,而且放大器的最大功率必須在負載為8歐揚聲器、總諧波失真小於1%條件下測定。國際電工委員會規定的總諧波失真的最低要求為:前級放大器為0.5%,合併放大器小於等於0.7%,但實際上都可做到0.1%以下:FM立體聲調諧器小於等於1.5%,實際上可做到0.5%以下;雷射唱機更可做到0.01%以下。由於測量失真度的現行方法是單一的正弦波,不能反映出放大器的全貌。實際的音樂信號是各種速率不同的複合波,其中包括速率轉換、瞬態回響等動態指標。故高質量的放大器有時還註明互調失真、瞬態失真、瞬態互調失真等參數。
(2)瞬態失真(TIM):將方波信號輸入到放大器後,其輸出波形包絡的保持能力來表達。如放大器的轉換速率不夠,則方波信號即會產生變形,而產生瞬態失真。主要反映在快速的音樂突變信號中,如打擊樂器、鋼琴、木琴等,如瞬態失真大,則清脆的樂音將變得含混不清。
(3)瞬態互調失真:將3.15kHz的方波信號與15kHz的正弦波信號按峰值振幅比4:1混合,經放大器後,新增加全部互調失真的產物有效值與原來正弦振幅的百分比。如放大器採用深度大迴環負反饋,瞬態互調失真一般較大,具體反映出聲音呆滯、生硬、無臨場感;反之,則聲音圓滑、細膩、自然。
失真條件
線性失真
先討論線性失真:從信號與系統的角度來考慮,所謂無失真傳輸,通過數學推導(有興趣可以參考〈信號與系統〉教材)可以得到兩個條件:
1,系統對幅度譜的作用僅為加權作用。
2,系統對相位譜的延遲與頻率成正比,既滿足常數群時延特性。這兩個結論是基於傅立葉分析的基本理論而得到的。如果它晦澀難懂,那么說簡單一點,大家看到的撥特圖(撥特圖包括幅度譜和相位譜兩部分),如果在其通頻帶範圍內,幅度譜和相位譜都是一直線,那這個系統(放大器就是一個電系統)就滿足無失真傳輸。現實中,無失真傳輸僅僅限於兩類系統,
1,電阻網路。
2,匹配的高頻傳輸線。而所有的放大器,在理論上都不可能成為無失真傳輸系統。放大器,如果忽略低頻截止頻率的影響(因為高頻截止頻率往往遠遠低頻截止頻率)為一低通濾波器。如果不忽略低頻截止頻率影響(因為低頻對音頻來說很重要),則為一帶通濾波器。由於電晶體為一電阻電容的混合參數所構成的器件(如各種形式參數模型所反應),由於電容的容抗中含有頻率參數,不同的頻率對應於不同的容抗,所以放大器不可能做到對其通頻帶內的所有信號放大倍數為常數。這樣,也就不滿足本段開始所述的條件
1。而且電容的電壓和電流並非同相位,所以不同的頻率就對應著不同的相移,就不能滿足條件
2。不滿足條件1的失真,我們稱做幅度失真(幅頻失真),不滿足條件2的失真,我們稱為相位失真(相頻失真)。根據傅立葉分析的基本理論,任何一周期信號都可以分解為其直流分量,基波分量和個次諧波分量的加權。所謂諧波,就是頻率為基波整數倍的餘弦信號。若為基波的N倍,即稱為N次諧波。可見,如果一個系統對不同頻率分量的放大倍數不同,那么對不同的諧波分量將有不同的放大倍數。當一個信號通過系統之後,各諧波分量的幅度發生了改變,加權後將不能真實反應原信號。這樣產生的失真,既為幅度失真。再者,從相位的角度來考慮,如果原信號的各次諧波通過這個系統,產生了不同的相移(表現在時域既為不同的延遲),則系統輸出的各次諧波加權之後,也不能真實反應原信號,這樣產生的失真,既為相位失真。這兩種失真,僅僅是各次諧波的幅度、相位產生了變化,但系統並沒有產生新的諧波頻率,所以稱為線性失真。降低線性失真的方法,可以展寬放大器的通頻帶,使其在工作頻率內(如音頻為20HZ-20KHZ)近似滿足無失真傳輸條件。但是,受電晶體特性影響(如截止頻率Ft)無限制展寬通頻帶是不可能的,而且在展寬通頻帶的同時,會帶來其它弊端,尤其是會引入噪聲。如熱噪等,其都和頻頻寬度相關。前人實驗表明,人耳對相頻失真表現得不敏感,但人眼對相頻特性及其敏感,所以不同的放大器,頻頻寬度視要求而定。
非線性失真
我們所常使用的各類電晶體等效模型,稱為小信號模型。因為當信號幅度非常小的時候,忽略了非線性因素的影響,將其進行線性等效。以上所討論的線性失真,皆為在這種等效前提下的討論。但事實上,無論的PN節(BJT電晶體)的E指數特性,還是場效應管(FET)的平方率特性,都是非線性的。如果考慮這種非線性對放大器的影響,則就有了非線性失真這個概念。非線性失真的種類繁多,但其本質都是由器件非線性影響所至。一般常有的度量標準,有總諧波失真,交叉調製失真,互相調製失真,順態互調失真等等。非線性失真的本質,就是產生的新的頻率分量。總諧波失真(THD):這也是在放大器中提的最多的一種失真。其定義方式為輸入單一頻率的餘弦信號,輸出的各次諧波總有效值和基波功率有效值之比的平方跟。THD的大小是功率放大器非常重要的指標,所謂高保真功率放大器,諧波失真在一般都在1%以內。一般而言,輸出功率越大,THD要做得好就越不容易。所以耳機放大器的諧波失真,看起來都是相當低的,其輸出功率小也是一定的原因。降低總諧波失真的方法,一般都是使用負反饋。反饋深度為1+AF,則加入負反饋之後失真就降為開環條件下的1/1+AF。負反饋是降低非線性失真行之有效的方法,也是模擬電子線路的精華之一,但是負反饋也並不是萬精油,會帶來犧牲系統增益,降低系統穩定性等總總弊端,也會引起其它的非線性失真(例如順態互調失真就別認為於深度負反饋息息相關)。交叉調製失
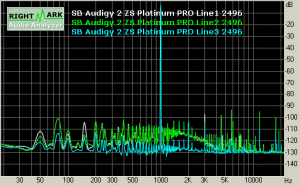 總諧波失真
總諧波失真
