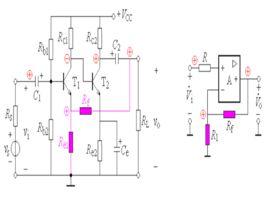
簡介
基本反饋方程
以基本單環放大器為例（圖6.3）
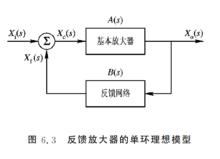反饋放大器的單環理想模型由開環放大倍數的定義，可以得到
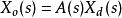反饋深度（式 1）
根據反饋係數的定義，可以將反饋信號表示為
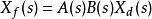反饋深度（式 2）
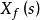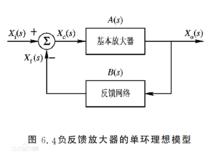
反饋深度對於負反饋情況，系統流圖中的 前應加入一個負號（圖6.4）
反饋深度將式1、式2代入閉環放大倍數的表示式
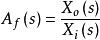反饋深度可以得到分析理想單環負反饋電路的重要公式
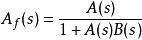反饋深度即引入負反饋後，放大電路的放大倍數閉環增益是無反饋時開環增益的A(s)/1+ A(s)B(s)倍
將A(s)B(s)=T(s)定義為環路增益，表示在反饋放大電路中，信號沿著放大器和反饋網路組成的環路傳遞一周后所得到的放大倍數。
反饋深度定義
定義分母1+ A(s)B(s)=F(s)為反饋深度。反饋深度是一個十分重要的參數，表示引入反饋後放大電路的放大倍數與無反饋時相比所變化的倍數。可以看到，引入負反饋後，閉環增益降低為無負反饋時的1/F倍。把反饋深|F|>>1時的負反饋稱為深度負反饋，此時
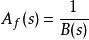反饋深度分類
反饋深度可以分為以下幾種情況：
(1)當(1+AF)遠大於1時，此時的反饋就叫深度負反饋，此時的負反饋增益等於1/F。分壓式共基極偏置放大電路就是一個深度負反饋放大電路
(2)當(1+AF)等於1時，則表明反饋效果為零。
(3)當(1+AF)遠小於1時，表明放大器的淨輸入量增大，放大倍數升高，這種反饋稱為正反饋。多用於振盪器。
(4)當(1+AF)等於0時，則表明閉環增益為無窮大，此時的放大器無輸入量，也有輸出量，放大器處於“自激振盪”狀態，嚴重時放大電路不能正常工作，必須消除。
特點
一般來說，反饋深度愈深，改善的效果愈顯著。但是，對於多級放大電路而言，負反饋深度太深可能會引起放大電路產生自激振盪，使放大電路失去放大作用，不能正常工作。
單級和兩級放大電路是穩定的，而三級或三級以上的負反饋放大電路，只要有一定的反饋深度，就可能產生自激振盪，因為在低頻段和高頻段可以分別找出一個滿足相移為180度的頻率（滿足相位條件），此時如果滿足幅值條件|AF|=1，則將產生自激振盪。因此對三級及三級以上的負反饋放大電路，必須採用校正措施來破壞自激振盪，達到電路穩定工作目的。
