概述
S轉換(s-transform),或S變換是一種時頻分析的工具。
和其他時頻分析工具一樣,透過S轉換,我們可以同時從時域以及頻域觀察一個信號的能量分布。
S轉換的特別之處在它既保持與傅立葉變換的直接關係,又可在不同頻率有不同的解析度。此外,S轉換與小波轉換(wavelet transform)有密切的關係,或可視為連續小波轉換(continuous wavelet transform)的變形。
S轉換的清晰度略優於加伯轉換(Gabor transform),而不如韋格納分布(Wigner distribution function)、科恩克萊斯分布、改良式韋格納分布(Modified Wigner distribution function)。
定義
一個信號x(t)的S轉換 為
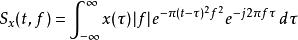 S轉換
S轉換其中窗函式為高斯窗函式
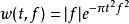 S轉換
S轉換另種表示-頻譜表示式
借著折積定理
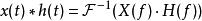 S轉換
S轉換S轉換能以頻域X(f) 表示,
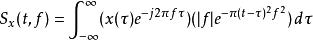 S轉換
S轉換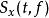 S轉換
S轉換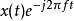 S轉換
S轉換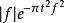 S轉換
S轉換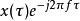 S轉換
S轉換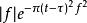 S轉換
S轉換這裡可將看成與的卷積,將以及分別取傅立葉變換可得
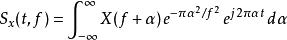 S轉換
S轉換逆S轉換(inverse S-transform)
S轉換可以沿著時間軸方向積分,將可以得到x(t)的頻譜 X(f)。推導如下,
利用Gaussian window所包含面積等於1的特性,
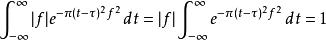 S轉換
S轉換因此,沿著時間軸t積分,
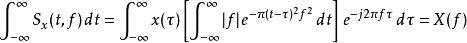 S轉換
S轉換這表示S頻譜是可逆的,同時也提供一個簡單的逆轉換。
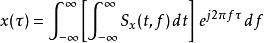 S轉換
S轉換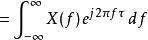 S轉換
S轉換濾波套用(Filtering)
S轉換如同其他時頻分析轉換,皆可以設計波器來達到消除噪聲留下訊號的功用,
利用逆S轉換,我們可以設計一個S域的濾波器U(t,f),對x(t)進行訊號處理
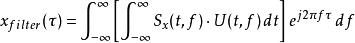 S轉換
S轉換離散時間S轉換
 S轉換
S轉換S轉換相較於加伯轉換,雖在清晰度有較好的改善,但也有其缺點,就是運算複雜度變高,積分的範圍會隨著
的增加而增加。因此,這裡利用上面推導的頻譜表示式來推導離散時間S轉換
頻譜表示式
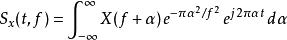 S轉換
S轉換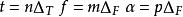 S轉換
S轉換令
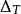 S轉換
S轉換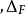 S轉換
S轉換表示取樣時間間隔表示取樣頻率
如果要使用FFT的方式來實作,必須另加條件
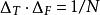 S轉換
S轉換首先先對x(t)做傅立葉變換得到 X(f)
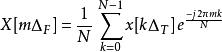 S轉換
S轉換接著帶入頻譜表示式中,
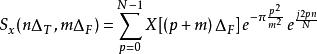 S轉換
S轉換當 m=0 時,S轉換就定義成
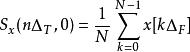 S轉換
S轉換S轉換特性
S轉換與加伯轉換(Gabor Transform)很相似,
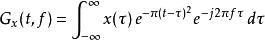 S轉換
S轉換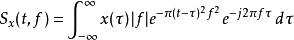 S轉換
S轉換唯一的不同就在於S轉換的Gaussian Window的寬度會隨著{\displaystyle f}改變。
S轉換一般式
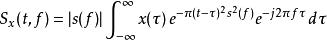 S轉換
S轉換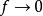 S轉換
S轉換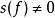 S轉換
S轉換s(f)是一個相對平緩的曲線,當時,
S轉換是一種運算量高的時頻分析工具,尤其在低頻部分,Gaussian Window寬度變寬,頻域解析度比加伯轉換來的好,所以S轉換對於低頻訊號分析比較有優勢。
例如:聲音訊號,人耳對高頻的部分沒有太特別的感覺,但在低頻部分卻比較敏感,如:中央Do = 262Hz,高八度Do = 512Hz 可以很清楚的聽出兩個不同的音, 但10000Hz 和 10170Hz對人來說差別不大,再說人耳對3KHz以內的聲音最敏感,所以能分析低頻訊號就顯得重要。
此時,就可以使用S轉換,來強調低頻訊號,而犧牲高頻訊號。
與韋格納分布的比較
韋格納分布是時頻分析工具中,具有高清晰度的一個,但最大的缺點是有交叉項(cross-term)的問題。若一個信號是由數個信號成分組合而成,那么使用韋格納分布來分析時就會受到兩兩信號成分之間的交叉項干擾,這將會產生一些不必要的噪聲。
一個信號x的韋格納分布為
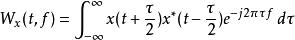 S轉換
S轉換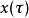 S轉換
S轉換交叉項是在積分中兩個x項相乘時產生的。S轉換的計算原理與韋格納分布不同,是直接對進行轉換,不會有交叉項的問題。
與加伯轉換的比較
加伯轉換的定義為
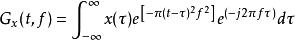 S轉換
S轉換我們知道加伯轉換是短時距傅立葉轉換的一種特殊形式,其中只要把短時距傅立葉轉換的窗函式用高斯函式來替代就成了加伯轉換;S轉換則可視為一種窗函式會隨f變化的加伯轉換;隨著頻率的升高,高斯函式在時域上的寬度會越來越窄,使得時域上的解析度會增加,反之犧牲頻域上的解析度。
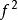 S轉換
S轉換加伯轉換和S轉換原理相同,兩者唯一不同的地方就是窗函式的和強度f,基本上都是由短時距傅立葉轉換延伸而來;兩者共有的好處是不會像韋格納分布一樣會有交叉項;又S轉換在低頻時的頻率解析度會優於加伯轉換。
與小波轉換的關係
連續小波轉換可以視為將一個信號對小波做相關(correlation):
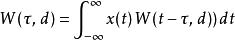 S轉換
S轉換而S轉換可以視為連續小波轉換乘上一個相位項:
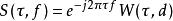 S轉換
S轉換而其用的母小波為:
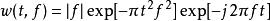 S轉換
S轉換