數字振盪器
高精度範圍
在正交數字混頻器中,採用數字頻率合成技術,可以將數字處理延續到正交調製之後或正交解調之前,濾波器和增益控制就可以用數字方法實現,I、Q兩路也就不會存在增益的不平衡,加上數控振盪器(NCO)的低正交誤差,可以使系統誤差降低到數據的最低比特(LSB)的高精度範圍。
調製靈活性
此外,正交數字混頻器更容易與數位訊號處理技術結合,使得數字調製更加靈活,進而實現軟體無線電所要求的軟體可更改的調製解調。 數控振盪器是正交數字混頻器的核心部分,它具有頻率解析度高、頻率變化速度快、相位可連續線性變化和生成的正弦P餘弦信號正交特性好等特點。而且NCO的相位、幅度均已數位化,可以直接進行高精度的數字調製解調。隨著數字通信的發展,傳送的數據速率越來越高。如何得到一個可數控的高頻載波信號是實現高速數字通信系統必須解決的問題。
數控振盪器的基本實現原理
數控振盪器的作用是產生正交的正弦和餘弦樣本。傳統方法是採用查表法(LUT),即事先根據各個正餘弦波相位計算好相位的正餘弦值,並按相位角度作為地址存儲該相位的正餘弦值,構成一個幅度P相位轉換電路(即波形存儲器)。在系統時鐘的控制下,由相位累加器對輸入頻率字不斷累加,得到以該頻率字為步進的數字相位,再通過相位相加模組進行初始相位偏移,得到要輸出的當前相位,將該值作為取樣地址值送入幅度P相位轉換電路,查表獲得正餘弦信號樣本。對於一個相位位數為n ,輸出信號幅度位數為M的數控振盪器,所需查找表大小為M×2n 。為了提高數控振盪器的頻率解析度,往往需要擴大波形存儲器的容量,造成存儲資源的大量消耗。而且,當需要外掛RAM 來存儲波形時,由於受到RAM讀取速度的影響,數控振盪器的輸出速率必然受到制約。因此,當需要設計高速、高精度的數控振盪器時,不宜採用查表法。
足夠的精度
為了避免使用大容量存儲器,可以考慮利用算法來產生正餘弦樣本。基於矢量鏇轉的CORDIC算法正好滿足了這一需求,該算法主要用於計算三角函式、雙曲函式及其它一些基本函式運算。它有線性的收斂域和序列的特性,只要疊代次數足夠,即可保證結果有足夠的精度。
運算公式
Walther JS於1971年提出了統一的CORDIC形式。假定初始向量V1(x1 ,y1)鏇轉角度θ後得到向量V2(x2,y2):
即:
若每次鏇轉的角度θ是正切值為2 的倍數,即θi=arctan(2-i),則cosθi=(1+2-2i)-1/2 。假設以δi代表矢量的鏇轉方向,+1表示逆時針鏇轉,-1表示順時針鏇轉,故第i 步鏇轉可用下式表示:
其中:(1+2-2i)-1/2為模校正因子。對於字長一定的運算,該因子是一個常數,用K表示,以16 bits字長為例,則:
可見,疊代運算不能使幅值比例因子恆為1。為了抵消因疊代產生的比例因子的影響,可將輸入數據X,Y校正後再參與運算,以避免在疊代運算中增加校正運算,降低CORDIC算法的速度。由此運算疊代式可以簡化成:
公式(5)運算僅通過加法器及移位器就可以實現。此外,若用Zi表示第i次鏇轉時與目標角度之差, 則:
經過n次鏇轉後,式(5)的n次疊代可以得到以下結果:
本文介紹的數控振盪器的設計是在式(7)的基礎上,給定x0=K ,y0=0,則疊代結果為:
將所需產生的角度值作為z0輸入,通過式(5)、(6)的疊代運算,疊代結果輸出的xn和yn就是所需要的三角函式值。
數控振盪器的FPGA實現
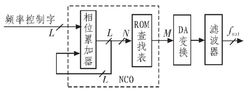 NCO
NCO圖1是數控振盪器的頂層電路。由圖可見,頻率控制字暫存器將接收到的的頻率控制字送入相位累加器,相位累加器對系統時鐘進行計數,每到達輸入頻率控制字的值即對相位進行累加,隨後將累加值送入相位相加器,與相位控制字暫存器接收到的初始相位進行相加,得到當前的相位值。其中,相位累加器是決定NCO性能的一個關鍵模組,可以利用FPGA器件的進位鏈實現快速、高效的電路結構。然而,由於進位鏈必須位於臨近的邏輯陣列塊CLB和邏輯單元LC內,所以長的進位鏈會減少其它邏輯使用的布線資源;同時,過長的進位鏈也會制約整個系統速度的提高。因此,設計中採用進位鏈和流水線技術相結合的辦法。所謂流水線技術,即把在一個時鐘內要完成的邏輯操作分成幾步較小的操作,並插入幾個時鐘周期來提高系統的數據吞吐率。採用以上做法實現的相位累加器既能保證具有較高的資源利用率,又能大幅提高系統的性能和速度。
經過上述相位的處理之後,即可獲得具有所設定初始相位的一定頻率的正餘弦相位序列,將此序列送入基於CORDIC算法的波形發生器,最終獲得兩路正交的正餘弦輸出序列。
NCO的頂層電路結構
CORDIC疊代算法的一種最直接的實現方法是,只設計一級CORDIC運算疊代單元,然後在系統時鐘的驅動下,將本級的輸出作為本級的輸入,通過同一級疊代完成運算。這種方法雖然很直觀,但是為了將計算結果提供給下一級運算而導致占用了大量的暫存器,帶來許多額外的資源消耗。而最大的缺點是運算速度較慢(需要n-1個時鐘周期才能輸出一個數據),不利於數據的高速實時處理。
因此在實際設計中,採用的是圖2所示的由16級CORDIC運算單元組成的流水線結構,正常工作時只需1個時鐘周期就能輸出1個數據,為數據實現高速實時處理提供了前提。每一級實現的功能是根據式(5)進行一次疊代,移位的位數等於當前的疊代級數,加減法選擇由該級中Z 的最高位(符號位)決定,得到下一級的X 、Y 和Z 的值。經過16級流水線運算後,Z的值變為0,X 和Y 的值則為初始值z0的餘弦和正弦值。每一級電路結構主要包括2個移位器和3個加(減)法器,級與級之間直接相連,不需要額外的暫存器。θi 的值為arctan(2-i),可將該小數轉換為二進制數後,存儲於存儲單元中,為每一級流水線提供查找表。若對於16級的流水線結構,則的範圍是0~15。
CORDIC疊代算法的流水線結構
設計中還應該注意疊代序列所能復蓋的角度範圍,若直接採用n 級疊代序列:0 ,1 ,2 ,…,n - 1 ,則疊代所能復蓋的角度範圍僅有- 99.9°~99.9°。本設計採用了增加疊代次數的方法來擴大角度復蓋範圍,即增加兩個i = 0 的疊代,將疊代序列擴展為0,0,0,1,2,…,n-1,從而使角度復蓋範圍也擴大到-π~π。
數控振盪器的仿真結果及性能分析
利用ALTERA公司的QuartusII軟體,採用VHDL硬體描述語言對上述數控振盪器結構進行描述,在Modlesim上通過功能仿真,結果正確后綜合出電路網表,最後將程式下載至ALTERA公司生產的Stratix器件EP1S20B780C6實現。
由於設計中採用了Stratix器件,該器件的32位加減器工作頻率可以達到90MHZ以上,為產生高速的正交信號提供高速可靠的的工作時鐘。考慮到NCO的工作時鐘瓶頸是在相位累加器,因此可以根據具體需要縮減相位累加器的位數來提高NCO的工作時鐘。
本文設計的NCO工作時鐘為100MHz,相位累加器的位數為16位,輸入的頻率控制字為4CCCH,根據公式:
其中:Φword為輸入的頻率控制字;fclk為工作時鐘;N為相位累加器位數,可算出NCO輸出的正餘弦信號的頻率;fout為30MHZ ;頻率解析度Δf ≈1.5 kHz。頻率解析度說明了若通過輸入頻率控制字來改變輸出正餘弦信號的頻率時,可以達到1.5 kHz 的最小步進。另外,也可以根據實際需要的頻率改變輸入頻率控制字值。當然,NCO輸出頻率的上限要受到Nyquist定律的限制,即fout的最大值為fclkP2,實際設計一般不大於0.4fclk。圖3為數控振盪器的部分仿真時序圖。
結語
研究了正交數字混頻器中數控振盪器的設計與實現方法,著重分析了如何在FPGA器件中利用CORDIC疊代算法產生正餘弦信號。結果表明,基於CORDIC疊代算法的數控振盪器,僅用移位暫存器和加法器就可產生正餘弦信號,不但省去了傳統NCO龐大的存儲器資源,而且保留了一般數控振盪器頻率解析度高、頻率變化速度快、相位可連續線性變化、生成的正弦P餘弦信號正交特性好等特點,非常適用於在正交數字混頻器中進行高速高精度的數字調製解調。
