研究現狀
1989 年,著名的密碼學家 Merkle提出了 Merkle 可信樹的思想。在 Merkle可信樹認證方法中,其關鍵是 Merkle 可信樹的構造以及認證路徑節點值的計算,一些學者針對提高 Merkle 可信樹的遍歷速度,即提高葉子節點認證路徑的查找效率,提出了一些 Merkle 可信樹遍歷算法的改進方案。
2003 年 MichaelSzydlo採用僅計算目前最緊迫需要計算的節點哈希值的方法來減少一次性存儲的節點哈希函式值,同時該方法減少了哈希函式值的計算量。
2004 年,Michael Szydlo採用儘量減少冗餘哈希函式值的計算的思路,更進一步的對Merkle 可信樹的遍歷算法進行了改進。
2005 年,Glen Nuckolls提出了混合可信樹的思想,降低了 Merkle 可信樹中認證路徑對樹高的依賴,在該方法中,認證路徑不再完全是可信樹中從葉子節點到根節點的路徑上的節點的兄弟節點。
2006 年,W.Eric Hall提出平行認證樹的思想,該方法是藉助外部設備以實現對多個葉子節點同時進行認證,縮短了葉子節點的認證時間,但是該方法對外部設備的要求較高,需要大的成本投入。
此外,在提高 Merkle 可信樹的簽名數量方面,Johannes Buchmann 提出了 CMSS方案,該方法增加了簽名的數量,但是密鑰產生的效率仍然很低下。
之後,Johannes Buchmann 又提出了 GMSS的思想,使得簽名的數量更進一步的增加。雖然對 Merkle 可信樹已經有了一些成果,但是如何進一步地提高 Merkle 可信樹認證的效率仍然有待進一步研究。
Merkle 可信樹認證思想
 Merkle 可信樹
Merkle 可信樹給定一組數據,現在需要在適度的記憶體需求下對這組數據進行認證。
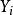 Merkle 可信樹
Merkle 可信樹為了認證(1≤ i ≤ n),一棵二叉樹被構造,該二叉樹被稱之為 Merkle 可信樹,二叉樹中每個節點都有一個值與之對應。二叉樹中的每個節點從根節點開始以層遍歷的方式被編號,即根節點為節點 1,任何中間節點 i 的孩子節點為節點2i和節點2i + 1。二叉樹中每個節點對應的值按照如下規則定義:
 Merkle 可信樹
Merkle 可信樹1. 葉子節點的值由的值得到。
2. 中間節點 i 的值由節點 2i 和節點 2i + 1的值得到。
由二叉樹節點對應的值的定義規則可知,節點 1 的值與整棵二叉樹的每個葉子節點的值都是相關聯的。中間節點 i 的值與以節點 i 為根的子樹的所有葉子節點對應的值有關。這種節點對應的值的相互依賴性使得任何一個葉子節點可以有選擇性的被認證。下面以一個例子說明 Merkle 可信樹的認證思想。
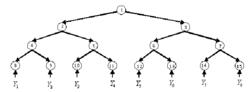 圖1 Merkle可信樹
圖1 Merkle可信樹如圖 1 構造了一棵 n = 8的 Merkle 可信樹:
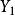 Merkle 可信樹
Merkle 可信樹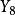 Merkle 可信樹
Merkle 可信樹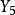 Merkle 可信樹
Merkle 可信樹節點 8 至節點 15 的值分別與至的值相對應,認證的過程如下:
1)節點 1 已經知道並且被認證。
2)節點 1 的值由節點 2 的值和節點 3 的值計算得到,傳送節點 2 和節點 3的值,並且讓接收者通過接收到的節點 2 和節點 3 的值計算節點 1 的值,驗證計算出的節點 1 的值是否正確。
3)接收者已經驗證了節點 3 的值,傳送節點 6 和節點 7 的値,並且讓接收者通過接收到的節點 6 和節點 7 的值計算節點 3 的值,驗證計算出的節點 3 的值是否正確。
4)接收者已經驗證了節點 6 的値,傳送節點 12 和節點 13 的值,並且讓接收者通過接收到的節點 12 和節點 13 的值計算節點 6 的值,驗證計算出的節點6 的值是否正確。
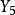 Merkle 可信樹
Merkle 可信樹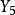 Merkle 可信樹
Merkle 可信樹5)接收者已經驗證了節點 12 的值。傳送,並且讓接收者通過的值計算節點 12 的值,驗證計算出的節點 6 的值是否正確。
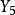 Merkle 可信樹
Merkle 可信樹6)接收者已經驗證了。
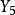 Merkle 可信樹
Merkle 可信樹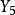 Merkle 可信樹
Merkle 可信樹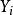 Merkle 可信樹
Merkle 可信樹事實上,以上一些值的傳送是沒有必要的,如節點 6 的值能夠通過節點 12和節點 13 的值計算得到。即不需要傳送節點 6 的値。類似的,節點 3 的值能夠從節點 6 和節點 7 的值計算得到。所以節點 3 沒有必要傳送。所以,實際上,認證節點僅僅需要驗證節點 1 的値和傳送、節點 13 的值、節點 7 的值、節點 2 的値。認證節點(1≤ i ≤ n)所需要的從根節點到葉子節點的節點路徑稱為認證路徑。如在圖1中,節點 8 的認證路徑為節點 9、節點 5、節點 3,實際上,認證路徑節點是指所有從認證葉子節點到根節點的節點的兄弟節點。
Merkle 可信樹是一棵完全二叉樹,完全二叉樹中的每個節點都有一個哈希函式值與之對應,葉子節點的哈希函式值是對需要認證的數據進行哈希運算得到的,而中間節點的哈希函式值是由其孩子節點的哈希函式值聯合進行哈希運算得到的。每個葉子節點數據的認證是通過認證路徑驗證根節點值得到的。
Merkle 可信樹數字簽名
下面簡要介紹基本的 Merkle 可信樹數字簽名(MSS)的過程。
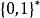 Merkle 可信樹
Merkle 可信樹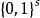 Merkle 可信樹
Merkle 可信樹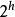 Merkle 可信樹
Merkle 可信樹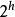 Merkle 可信樹
Merkle 可信樹令H:→是一個加密哈希函式,假設一個一次簽名方案已經給定。令h∈N,h 是 Merkle 可信樹的高。高度為 h 的二叉樹有個葉子節點,每個葉子節點對應一個一次簽名。這個一次簽名是通過一個 Merkle 可信樹數字簽名公鑰產生和認證的。整個簽名過程包括三個階段:密鑰對產生階段,簽名產生階段和認證階段。
MSS 密鑰對產生階段
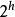 Merkle 可信樹
Merkle 可信樹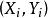 Merkle 可信樹
Merkle 可信樹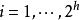 Merkle 可信樹
Merkle 可信樹 Merkle 可信樹
Merkle 可信樹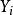 Merkle 可信樹
Merkle 可信樹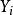 Merkle 可信樹
Merkle 可信樹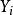 Merkle 可信樹
Merkle 可信樹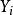 Merkle 可信樹
Merkle 可信樹首先,產生個一次簽名密鑰對,。是一次簽名的私鑰,是一次簽名的認證密鑰。MSS 的私鑰是一次簽名私鑰序列。為了計算 MSS 的公開密鑰,構造一棵二叉可信樹,將每個認證密鑰看做是一個比特字元串,可信樹的葉子節點對應的值是認證密鑰的哈希值H(),二叉樹的每箇中間節點的哈希函式值都是將其孩子節點的哈希函式值連線起來進行哈希運算得到的。MSS 的公開密鑰是可信樹的根節點值。
MSS 簽名產生階段
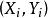 Merkle 可信樹
Merkle 可信樹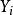 Merkle 可信樹
Merkle 可信樹一次簽名密鑰對被繼續使用。下面以使用第 i 個密鑰對簽名數據 d 為例來說明 MSS 數字簽名的過程。簽名包含序列號 i 和第i 個認證密鑰,一次簽名σ 由一次簽名算法產生,MSS 簽名由序列號 i、認證密鑰、一次簽名、和與序列號 i 對應的認證路徑 A 組成,認證路徑是由一系列節點值組成的。
認證階段
為了認證一個 MSS 簽名(i , Y , σ , A),認證方首先使用認證密鑰Y 認證一次簽名σ 。如果認證失敗,則認證方認為這個簽名是不合法的,如果認證成功,則認證方使用認證路徑來檢驗認證密鑰 Y 的合理性。如果使用認證密鑰 Y 和認證路徑計算出的根節點值與公開密鑰的值相同,則認證者接受這個簽名。
Merkle 可信樹遍歷過程
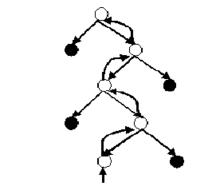 圖2 認證路徑圖
圖2 認證路徑圖Merkle 可信樹是一棵完全二叉樹,套用 Merkle 可信樹需要計算並輸出Merkle 可信樹的每個葉子節點的認證路徑上的節點的哈希函式值,一個葉子節點的認證路徑是指從該葉子節點到根節點的路徑上經過的節點的兄弟節點。如圖 2 所示:
在圖 2 中,黑色節點即為箭頭所指向的節點的認證路徑節點。弧形曲線指向的路徑即為從葉子節點到根節點的路徑。
下面以一個 n = 8的 Merkle 可信樹為例來說明一個簡單的 Merkle 可信樹遍歷過程。
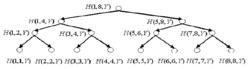 圖3 Merkle 可信樹遍歷圖
圖3 Merkle 可信樹遍歷圖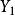 Merkle 可信樹
Merkle 可信樹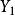 Merkle 可信樹
Merkle 可信樹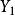 Merkle 可信樹
Merkle 可信樹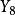 Merkle 可信樹
Merkle 可信樹在圖 3 中,H (1,1, Y )對應於節點的哈希函式值,對於圖 3 所示的 Merkle可信樹,遍歷方案的任務是從葉子節點開始依次輸出從到的認證路徑。
對於上圖 3所示的 Merkle 可信樹的各個節點的認證路徑如下圖 4所示。
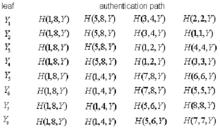 圖4 需計算的認證路徑節點圖
圖4 需計算的認證路徑節點圖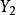 Merkle 可信樹
Merkle 可信樹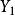 Merkle 可信樹
Merkle 可信樹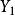 Merkle 可信樹
Merkle 可信樹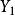 Merkle 可信樹
Merkle 可信樹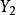 Merkle 可信樹
Merkle 可信樹要計算葉子節點對應的認證路徑節點值,就必須計算認證路徑上每個節點的哈希函式值,如計算節點的認證路徑節點值,需要計算節點H (1,8, Y )、H (5,8, Y )、 H (3, 4, Y )、 H (2, 2, Y )的值。依次類推,要計算出每個節點的認證路徑都必須重新計算出其對應每個節點的哈希函式值。如對於節點和,它們的認證路徑上都包括了 H (1,8, Y )和 H (5,8, Y )的值,即在計算和的認證路徑節點值的過程中, H (1,8, Y )和 H (5,8, Y )的值被重複計算了。所以如果能夠利用前個葉子節點的認證路徑節點值,那么整個計算量會減少。如圖5所示。
 圖5 簡化後需計算的認證節點圖
圖5 簡化後需計算的認證節點圖最佳化一個遍歷方案的目標是儘量減少冗餘的節點的哈希函式值的計算量,即縮短認證路徑節點值的輸出時間。顯而易見,當整棵 Merkle可信樹的節點的哈希函式值都被存儲起來時,節點計算是沒有冗餘的,但是對於一棵龐大的Merkle 可信樹而言,要存儲所有節點的哈希函式值,需要大量的空間消耗,這是不合理的。所以一個好的 Merkle 可信樹遍歷方案,在減少冗餘的計算量的同時,也要考慮空間存儲的最最佳化。
