人物生平
家庭背景
個人照片1854年4月29日，亨利·龐加萊出生於法國南錫一個學者家庭中。龐加萊家族在法國擁有極高聲望，龐加萊的父母親都出身於法國的顯赫世家，幾代人都居住在法國東部的洛林。他的祖父曾在拿破崙政權下的聖康坦部隊醫院供職，1817年在魯昂定居，先後生下兩個兒子，大兒子萊昂·龐加萊即為龐加萊的父親。龐加萊的父親和姐夫都是南錫大學醫學院的教授。他的母親是一位善良、才華出眾、很有教養的女性，一生的心血全部傾注到教育和照料孩子身上。龐加萊的兩個堂兄弟是法國政界的著名人物：雷蒙·龐加萊是法蘭西學院院士，並於1913-1920年間任法國總統；呂西·龐加萊曾任法國民眾教育與美術部長，負責中等教育工作。
因為視力極差，所以龐加萊在音樂和體育課上表現一般，除此之外，龐加萊在各方面都稱得上是成績優異。龐加萊的數學才華在上大學之前已經顯現出來。他的數學教師形容他是一隻“數學怪獸”，這隻怪獸席捲了包括法國高中學科競賽第一名在內的幾乎所有榮譽。
童年生活
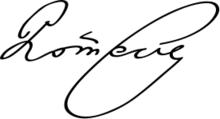龐加萊的簽名龐加萊的童年主要接受母親的教育。他的超常智力使他成為早熟的兒童，不僅接受知識極為迅速，而且口才也很流利。但不幸的事發生了：五歲時患了一場白喉病、九個月後喉頭壞了，致使他的思想不能順利用口頭表達出來，並成為一位體弱多病的人。儘管如此，龐加萊還是樂意玩耍遊戲，喜歡跳舞。當然，劇烈的運動他是無法進行的。
才華初展
龐加萊特別愛好讀書，讀書的速度快得驚人，而且能對讀過的內容迅速、準確、持久地記住。他甚至能講出書中某件事是在第幾頁第幾行中講述的。龐加萊還對博物學發生過特殊的興趣，《大洪水前的地球》一書據說給他留下了終身不忘的印象。他對博物學的興趣也很濃，歷史、地理的成績也很優異。他在兒童時代還顯露了文學才華，有的作文被老師譽為“傑作”。
求學生涯
1873年1862年龐加萊進入南錫中學讀書。初進校時雖然他的各科學習成績十分優異，但並沒有對數學產生特殊的興趣。對數學的特殊興趣大約開始於15歲，並很快就顯露了非凡才能。從此，他習慣於一邊散步，一邊在腦中解數學難題。這種習慣一直保持終身。
1870年7月19日爆發的普法戰爭使得龐加萊不得不中斷學業。法國戰敗了，法國的許多城鄉被德軍洗劫一空並被德軍占領。為了了解時局，他很快學會了德文。他親眼看到的德軍的暴行，成了一個熾熱的愛國者。
恢復學業
亨利·龐加萊1871年，龐加萊繼續學業。
1872年龐加萊兩次榮獲法國公立中學生數學競賽頭等獎，從而於1873年被高等工科學校作第一名錄取。據說，在南錫中學讀書時，他的老師就譽稱他為“數學巨人”。高等工科學校為了測試他的數學才能還特意設計了一套“漂亮的問題”，一方面要考出他的數學天才；另一方面也為了避免40年前伽羅瓦的教訓重演。
1873年，龐加萊進入巴黎綜合理工大學(école Polytechnique)，在那裡他得以從事他擅長的數學，師從著名數學家查爾斯·厄米特，並發表了他第一篇學術論文。後來龐加萊繼續跟隨厄米特攻讀博士學位。
大學研究
1879年1875年前後，龐加萊從理工大學畢業，進入南錫礦業大學繼續學習數學和採礦。畢業後，他加入了法國礦業集團(CorpsdesMines)成為法國東北部礦產區的一名巡視員，與此同時，龐加萊繼續在厄米特的指導下從事研究。在他一生的大部分時間裡，龐加萊都不曾放棄他的工程事業，他在1881至1885年間負責北方鐵路的建設工作，數年後成為法國礦業集團的總工程師，最後在總監的位置上退休。
1875年～1878年，龐加萊在高等工科學校畢業後，又在國立高等礦業學校學習工程，準備當一名工程師。但他卻缺少這方面的勇氣，且與他的興趣不符。
1879年8月1日，龐加萊撰寫了關於微分方程方面的博士論文，獲得了巴黎大學博士學位。然後到卡昂大學理學院任講師。
1881年任巴黎大學教授，直到去世。先後講授數學分析、光學、電學、流體平衡、電學中的數學、天文學、熱力學等課程。這樣，龐加萊一生的科學事業就和巴黎大學緊緊地聯在一起了。
1911年第一次索爾維會議上與居里夫人1887年龐加萊當選為法國科學院院士。1887年入選法國科學院，後任院長，並於1906年被選為法蘭西學院院士，這是法國學者的最高榮譽。
1899年因研究天體力學中的三體問題獲奧斯卡二世（OscarⅡ）獎金。
1906年龐加萊當選為法國科學院院長.
1908年以作家身份（散文家）成為法蘭西學院院士。
1908年龐加萊因前列腺增大而未能前往羅馬，雖經義大利外科醫生作了手術，使他能繼續如前一樣精力充沛地工作，但好景不長。
不幸辭世
1912年春天，龐加萊再次病倒了，7月9日作了第二次手術；7月17日在穿衣服時，突然因血栓梗塞，在巴黎逝世，終年僅58歲。
主要成就
龐加萊的研究涉及數論、代數學、幾何學、拓撲學等許多領域，最重要的工作是在函式論方面。他早期的主要工作是創立自守函式理論（1878）。他引進了富克斯群和克萊因群，構造了更一般的基本域。他利用後來以他的名字命名的級數構造了自守函式，並發現這種函式作為代數函式的單值化函式的效用。
1883年，龐加萊提出了一般的單值化定理（1907年，他和克貝相互獨立地給出完全的證明）。同年，他進而研究一般解析函式論，研究了整函式的虧格及其與泰勒展開的係數或函式絕對值的增長率之間的關係，它同皮卡定理構成後來的整函式及亞純函式理論發展的基礎。他又是多複變函數論的先驅者之一。
龐加萊為了研究行星軌道和衛星軌道的穩定性問題，在1881～1886年發表的四篇關於微分方程所確定的積分曲線的論文中，創立了微分方程的定性理論。他研究了微分方程的解在四種類型的奇點（焦點、鞍點、結點、中心）附近的性態。他提出根據解對極限環（他求出的一種特殊的封閉曲線）的關係，可以判定解的穩定性。
1885年，瑞典國王奧斯卡二世設立“n體問題”獎，引起龐加萊研究天體力學問題的興趣。他以關於當三體中的兩個的質量比另一個小得多時的三體問題的周期解的論文獲獎，還證明了這種限制性三體問題的周期解的數目同連續統的勢一樣大。
這以後，他又進行了大量天體力學研究，引進了漸進展開的方法，得出嚴格的天體力學計算技術。
龐加萊這一工作究竟給N體問題的解決以及動力系統的研究帶來巨大而無比深刻的影響：
第一，龐加萊證明了對於N體問題在N大於二時，不存在統一的第一積分（uniform first integral）。也就是說即使是一般的三體問題，也不可能通過發現各種不變數最終降低問題的自由度， 把問題化簡成更簡單可以解出來的問題，這打破了當時很多人希望找到三體問題一般的顯式解的幻想。在一百年後學習微分方程課的人大多在第二個星期就從老師那裡知道絕大多數微分方程是沒法找到定量的解的，但一般都能從定性理論中了解更多解的性質，甚至可以通過計算機“看到”解的形狀行為。而在龐加萊的年代，大多數數學家更熱衷於用代數或冪函式方法找到解，使用定性方法和幾何方法來討論微分方程就是起源於龐加萊對於N體問題的研究，這徹底改變人們研究微分方程的基本想法。
第二，為了研究N體問題，龐加萊發明了許多全新的數學工具。例如他完整地提出了不變積分（invariant integrals) 的概念，並且使用它證明了著名的回歸定理（recurrence theorem）。另一個例子是他為了研究周期解的行為，引進了第一回歸映象（first return map）的概念，在後來的動力系統理論中被稱為龐加萊映象。還有象特徵指數（characteristic expontents），解對參數的連續依賴性（continuous dependence of solutions with respect to parameters）等等。所有這些都成為了現代微分方程和動力系統理論中的基本概念。
亨利·龐加萊第三，龐加萊通過研究所謂的漸近解（asymptotic solutions），同宿軌道 (homoclinic orbits) 和異宿軌道（hetroclinic orbits），發現即使在簡單的三體問題中，在這樣的同宿軌道或者異宿軌道附近，方程的解的狀況會非常複雜，以至於對於給定的初始條件，幾乎是沒有辦法預測當時間趨於無窮時，這個軌道的最終命運。事實上半個世紀後，後來的數學家們發現這種現象在一般動力系統中是常見的，他們把它叫做穩定流形（stable manifold）和不穩定流形（unstable manifold）正態相交（intersects transversally）所引起的同宿糾纏（homoclinic tangle），而這種對於軌道的長時間行為的不確定性，數學家和物理學家稱之為混沌（chaos）。龐加萊的發現可以說是混沌理論的開創者。
龐加萊還開創了動力系統理論，1895年證明了“龐加萊回歸定理”。他在天體力學方面的另一重要結果是，在引力作用下，轉動流體的形狀除了已知的旋轉橢球體、不等軸橢球體和環狀體外，還有三種龐加萊梨形體存在。
龐加萊對數學物理和偏微分方程也有貢獻。他用括去法（sweepingout）證明了狄利克雷問題解的存在性，這一方法後來促使位勢論有新發展。他還研究拉普拉斯運算元的特徵值問題，給出了特徵值和特徵函式存在性的嚴格證明。他在積分方程中引進復參數方法，促進了弗雷德霍姆理論的發展。
龐加萊對現代數學最重要的影響是創立組合拓撲學。
1892年他發表了第一篇論文，1895～1904年，他在六篇論文中建立了組合拓撲學。他還引進貝蒂數、撓係數和基本群等重要概念，創造流形的三角剖分、單純複合形、重心重分、對偶複合形、複合形的關聯繫數矩陣等工具，藉助它們推廣歐拉多面體定理成為歐拉—龐加萊公式，並證明流形的同調對偶定理。
龐加萊的思想預示了德·拉姆定理和霍奇理論。他還提出龐加萊猜想，在“龐加萊的最後定理”中，他把限制性三體問題的周期解的存在問題，歸結為滿足某種條件的平面連續變換不動點的存在問題。
龐加萊在數論和代數學方面的工作不多，但很有影響。他的《有理數域上的代數幾何學》一書開創了丟番圖方程的有理解的研究。他定義了曲線的秩數，成為丟番圖幾何的重要研究對象。他在代數學中引進群代數並證明其分解定理。第一次引進代數中的左理想和右理想的概念。證明了李代數第三基本定理及坎貝爾—豪斯多夫公式。還引進李代數的包絡代數，並對其基加以描述，證明了龐加萊—伯克霍夫—維特定理。
龐加萊對經典物理學有深入而廣泛的研究，對狹義相對論的創立有貢獻。早於愛因斯坦，龐加萊在1897年發表了一篇文章“The Relativity of Space”〈空間的相對性〉，其中已有狹義相對論的影子。
1898年，龐加萊又發表《時間的測量》一文，提出了光速不變性假設。
1902年，龐加萊闡明了相對性原理。
1904年，龐加萊將洛倫茲給出的兩個慣性參照系之間的坐標變換關係命名為‘洛倫茲變換’。
再後來，1905年6月，龐加萊先於愛因斯坦發表了相關論文：《論電子動力學》。 他從1899年開始研究電子理論，首先認識到洛倫茨變換構成群（1904年），第二年愛因斯坦在創立狹義相對論的論文中也得出相同結果。
龐加萊的哲學著作《科學與假設》、《科學的價值》、《科學與方法》也有著重大的影響。他是約定主義哲學的代表人物，認為科學公理是方便的定義或約定，可以在一切可能的約定中進行選擇，但需以實驗事實為依據，避開一切矛盾。在數學上，他不同意羅素、希爾伯特的觀點，反對無窮集合的概念，贊成潛在的無窮，認為數學最基本的直觀概念是自然數，反對把自然數歸結為集合論。這使他成為直覺主義的先驅者之一。
1905年，匈牙利科學院頒發一項獎金為10000金克朗的鮑爾約獎。這個獎是要獎給在過去25年為數學發展做出過最大貢獻的數學家。由於龐加萊從1879年就開始從事數學研究，並在數學的幾乎整個領域都做出了傑出貢獻，因而此項獎又非他莫屬。
龐加萊定理
關於力學體系運動可逆性（或可復性）的定理。因由J.-H.龐加萊證明，故名。它指出，力學體系經過足夠長的時間後總可以回復到初始狀態附近。
1872年玻耳茲曼在研究實際熱力學過程的不可逆性即熱力學第二定律的微觀本質時，曾根據非平衡態的分布函式f（r，v，t）定義了一個函式H，並證明在孤立系統以非平衡態趨於平衡態的過程中，H隨時間單調下降，在平衡態達到最小值，這就是H定理。玻耳茲曼認為，H函式與熵對應，H的減少與熵的增大對應 ，H定理為熱力學第二定律提供了統計解釋。但是龐加萊定理似乎與H定理相矛盾。根據龐加萊定理，當H函式隨時間單調地減少之後，只要經過足夠長的時間，總可以重新增大，回復到初始的數值。對此，玻耳茲曼的回答是，H定理具有統計性質，即非平衡態總是以絕對優勢的機率趨於平衡態，逆過程並非完全不可能，只是機率極其微小。
龐加萊猜想
亨利·龐加萊主條目：龐加萊猜想
1904年，龐加萊在一篇論文中提出了一個看似很簡單的拓撲學的猜想：在一個三維空間中，假如每一條封閉的曲線都能收縮到一點，那么這個空間一定是一個三維的圓球。但1905年發現其中的錯誤，修改為：“任何與n維球面同倫的n維封閉流形必定同胚於n維球面。”後來這個猜想被推廣至三維以上空間，被稱為“高維龐加萊猜想”。
大於等於五維的龐加萊猜想被史蒂芬·斯梅爾證明；
四維的龐加萊猜想被麥可·弗里德曼證明；
三維的龐加萊猜想被俄羅斯數學家佩雷爾曼於2002-2003年證明。
他們分別獲得1966年，1986年和2006年菲爾茲獎。
獲獎記錄
英國皇家天文學會金質獎章（1900年）
布魯斯獎（1911年）
人物評價
概述
亨利·龐加萊阿達馬這位曾在函式論、數論、微分方程、泛函分析、微分幾何、集合論、數學基礎等領域做出過傑出貢獻的法國數學家認為，龐加萊“整個地改變了數學科學的狀況，在一切方向上打開了新的道路。”
羅素認為，本世紀初法蘭西最偉大的人物就是亨利·龐加萊。“當我最近在蓋·呂薩街龐加萊通風的休息處拜訪他時，……我的舌頭一下子失去了功能，直到我用了一些時間（可能有兩、三分鐘）仔細端詳和承受了可謂他思想的外部形式的年輕面貌時，我才發現自己能夠開始說話了。”
這位“如此美貌，如此年輕”的孩子，竟然是那些洪水般湧來、預示了柯西的一個後繼者的到來的論文作者，這是創辦《美國數學雜誌》的英國數學家西爾維斯特於1885年見到龐加萊的心情寫照。
龐加萊逝世80年來的歷史告訴我們，羅素、西爾維斯特、阿達馬等的論斷是多么正確！龐加萊一生髮表的科學論文約500篇、科學著作約30部，幾乎涉及到數學的所有領域以及理論物理、天體物理等的許多重要領域。
亨利·龐加萊談起龐加萊，大部分數學家都會馬上想起一個著名的評價：龐加萊是最後一個數學全才，即指其為最後一個在數學所有分支領域都造詣深厚的數學家。同樣著名的還有龐加萊本人的一句名言：數學家是天生的，而不是造就的。在龐加萊之前最近一個被稱為數學全才的是高斯(Gauss)。
除了是一名數學家之外，龐加萊還是一位影響深遠的物理學家，受惠於他的後人中包括當時正致力於完善狹義相對論的愛因斯坦。
三體問題，一鳴驚人
1885年，在剛創刊不久的瑞典數學雜誌ActaMathematica的第七卷上出現了一則引人注目的通告：為了慶祝瑞典和挪威國王奧斯卡二世在1889年的六十歲生日，ActaMathematica將舉辦一次數學問題比賽，懸賞2500克朗和一塊金牌。比賽的題目有四個，其中第一個就是找到多體問題的所有解。這是天體物理學中三體問題的一個推廣。而龐加萊在讀博士期間就已經開始研究太陽系中的多體問題。
但龐加萊最終卻沒有成功給出一個完整的解答，因為他發現這個系統的演變經常是混沌的，“混沌”是說如果初始狀態有一個小的擾動，例如一個體的初始位置有一個小的偏移，則後來的狀態可能會有極大的不同。也就是說，如果該小變動不能被我們的測量儀器所探測，則我們不能預測最終狀態為何。他的工作令評審印象深刻，因此還是在1888年贏得了獎金，時年34歲。
這是龐加萊學術生涯中第一個重要的獎項，1888年五月龐加萊在比賽截止日期前交上了他的論文，六個月後他就被宣布為獲勝者。評審維爾斯特拉斯很有預見地指出這篇論文將開創天體力學歷史上的一個新紀元。
數學、物理界的“十項全能”
從1881年開始直到其去世，龐加萊都在巴黎索邦大學任教，他曾教授過的課程包括物理、實驗力學、數學物理、機率論、天體力學和天文學。一個有趣的小插曲足以證明龐加萊在當時的地位：當軍政部長下令砍掉“沒用的天文學”課程時，龐加萊說“我來教這門課”，官員們就只好閉嘴了，因為誰也不敢阻攔龐加萊開設任何科學課程。
龐加萊的一生中在數學和物理的各個領域都有建樹，其中以其本人命名的科學發現就有龐加萊球面、龐加萊映射、龐加萊引理等。曾有人說：把一個微分幾何學家和廣義相對論學家從睡夢中搖醒，問他什麼是龐加萊引理。假如答不出來，那他一定是假的。
值得指出的是，以龐加萊命名的發現在其去世後仍然沒有停止：月亮上的一個火山口和一顆小行星都以他的名字命名。
在三體問題之後，1893年龐加萊參加了法國經度局，參與了把全世界的時間同步的活動。在1897年，他支持了一個沒有成功的把弧度測量十進制化進而把時間和經度十進制化的建議。這項工作導致他考慮高速移動的鐘如何互相同步的問題。1898年龐加萊闡述了相對論基本原理，根據這個原理，沒有機械或電磁試驗可以區分勻速運動的狀態和靜止的狀態。和荷蘭物理學家洛倫茲的合作中，他把時間的物理推向極限來解釋快速運動的電子的行為。這項工作最終由愛因斯坦完成。
“暗戰”愛因斯坦
在愛因斯坦之前，物理學家洛倫茲和數學家龐加萊都已經在這個方向上作了大量的工作，但龐加萊似乎無法接受愛因斯坦的狹義相對論，雖然兩個人的結果是幾乎一樣的。因此龐加萊雖然一輩子作了不少關於相對論的演講，但是他從來就沒提起過愛因斯坦與相對論這兩個詞。愛因斯坦不僅不引用龐加萊的工作，並宣稱從未讀過。當愛因斯坦的母校ETH(蘇黎世理工學院)要聘請愛因斯坦當教授時，龐加萊寫了一封信，大大地誇獎了愛因斯坦一番，最後一段話非常微妙：“我不認為他的預言都能被將來驗證，他從事的方向那么多，因此我們應該會想到，他的某些研究會走向死胡同。但在同時，我們有希望認為他走的某一個方向會獲得成功，而某一個成功，就足夠了。”
龐加萊於1912年去世，有個數學界的組織者給愛因斯坦去了一封信，說要出個紀念文集來紀念龐加萊，愛因斯坦拖了四個月才回信說，由於路上的耽擱，信剛剛收到，估計已經晚了，偏偏這位組織者不死心，說晚了也沒關係，你寫了就行。於是愛因斯坦又過了兩個半月回信說，由於事務繁忙，實在沒力氣寫了，然後不了了之。
但愛因斯坦最終在1921年的講演中公正地肯定了龐加萊對相對論的貢獻。愛因斯坦評價龐加萊為相對論先驅之一，他這么說：洛倫茲已經認出了以他命名的變換對於麥克斯韋方程組的分析是基本的，而龐加萊進一步深化了這個遠見……
後世紀念
月球上的龐加萊火山口
小行星：2021龐加萊
龐加萊大學
