簡介
在計算機科學中,形式文法是 Kuroda 範式的,若且唯若所有產生規則都有如下形式:
AB → CD
A → BC
A → B
A → α
這裡的 A, B, C 和 D 是非終結符而 α 是終結符。
所有 Kuroda 範式的文法都是單調的,因此生成上下文有關語言。反過來說,所有不生成空串的上下文有關語言都可以被 Kuroda 範式的文法所生成。
參見
巴科斯範式
巴科斯範式(英語:Backus Normal Form,縮寫為BNF),又稱為 巴科斯-諾爾範式(英語:Backus-Naur Form,縮寫同樣為BNF,也譯為 巴科斯-瑙爾範式、 巴克斯-諾爾範式),是一種用於表示上下文無關文法的語言,上下文無關文法描述了一類形式語言。它是由約翰·巴科斯(John Backus)和彼得·諾爾(Peter Naur)首先引入的用來描述計算機語言語法的符號集。
儘管巴科斯範式也能表示一部分自然語言的語法,它還是更廣泛地使用於程式設計語言、指令集、通信協定的語法表示中。大多數程式設計語言或者形式語義方面的教科書都採用巴科斯範式。在各種文獻中還存在巴科斯範式的一些變體,如擴展巴科斯範式EBNF 或擴充巴科斯範式ABNF。
喬姆斯基範式
在計算機科學中,一個形式文法是 Chomsky 範式的,若且唯若所有產生規則都有如下形式:
A→BC
A→ α
S→ ε
這裡的 A, B和 C是非終結符,α 是終結符(表示常量值的符號), S是開始符號,而 ε 是空串。還有, B和 C都不可以是開始符號。
所有的 Chomsky 範式的文法都是上下文無關,反過來,所有上下文無關文法都可以有效的變換成等價的 Chomsky 範式的文法。
除了(在文法可能生成空串的時候包括的)可選規則 S→ ε 是例外,Chomsky 範式的文法的所有規則都是擴張的,就是說在字元串的整個導出過程中,每個終結符和非終結符的字元串比起前面導出的字元串要么同樣長度要么多出一個元素。長度 n 的字元串的導出總是精確的 2n-1 步長。
Chomsky 範式得名於諾姆·喬姆斯基,他是發明喬姆斯基層級的美國語言學家。
格雷巴赫標準式
在計算機科學中,聲稱一個上下文無關文法是 Greibach 標準式(範式)(GNF)的意味著所有的產生規則都有如下形式:
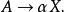 黑田範式
黑田範式或
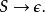 黑田範式
黑田範式這裡的 A是非終結符,α 是終結符, X是不包括開始符號的非終結符的(可能為空)的序列, S是開始符號,而 ε是空串。可觀察出這種文法沒有左遞歸。所有上下文無關文法口可以被轉換成等價的 Greibach 範式的文法。(某些定義不認可第二種形式的規則,在這種情況下能生成空串的上下文無關文法不能被如此轉換。)這可以被用來證明所有上下文無關語言可以被非確定下推自動機所接受。給定 GNF 的一個文法和長度為 n的符合這個文法的一個可導出的字元串,任何自頂向下分析器將在深度 n停機。 Greibach 範式得名於Sheila Greibach。
