簡介
粘性流動是自然界和工程技術中普遍存在的流動過程。例如,近地面和水面的大氣邊界層中的空氣流動,空氣繞過飛機、汽車和地面建築物的流動,水繞橋墩、船舶和近海結構物的流動,流體在管道和渦輪機械中的流動,機器軸承中潤滑液的流動,人體血管中的血液流動等都是粘性流動。
影響因素
所謂黏性流動是指非晶態固體和液體在很小外力作用下,會發生沒有確定形狀的變形,並且在外力去除之後,形變不能回復。
純粘性流動服從牛頓黏性流動定律:σ=η ·(dε/dt)。式中,σ為應力;(dε/dt)為應變速率;η為黏度係數,它反映了流體的內摩擦力,即流體流動的難易程度,其單位為Pa ·s。在應力的持續作用下,鏈段沿外力方向運動取向,伴隨發生分子鏈間的位移,具有不可逆性,這稱為黏性流動。
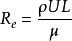 黏性流動
黏性流動影響粘性流動狀態的主要參數是雷諾數 Re。式中 ρ、 μ分別為流體的密度和動力粘性係數; U、 L分別為流動的特徵速度和特徵長度。
在幾何形狀相似的管道流動的液體,不論它們的液體的平均流速,液體密度如何,只要Re相同,它們的流動類型就相同。Re<1000時,液體流動為層流;Re>1500時,流體流動為湍流;當1000<Re<1500,不穩定。
當雷諾數很小時,粘性影響遍及整個流場;當雷諾數很大時,明顯的粘性效應只局限於物體表面附近的一層很薄的流體(即邊界層)中。另外,當雷諾數較小時,粘性流動為規則的層流;當雷諾數較大時,粘性流動則為不規則的湍流。
運動方程
描述粘性流動的運動方程是納維-斯托克斯方程。對於圓管和楔形槽中的液體層流,G.H.L.哈根和J.-L.-M.泊肅葉等已從實驗歸納出它們的規律,後來證明與精確解符合(見管流)。關於雷諾數比 1小得多的繞浸沒物體的蠕動流,G.G.斯托克斯等求得一些近似解,包括著名的斯托克斯圓球阻力公式,即阻力同速度成正比(見斯托克斯流動)。對於大雷諾數情形,L.普朗特建立了有效的邊界層近似理論。湍流是粘性流動中比較困難而又具有重要實際意義的問題。解決有關湍流的工程技術問題有混合長和各種模式的半經驗理論(見湍流理論)。理論研究方面則發展了統計理論。在解複雜的粘性流動問題(包括分離流、湍流)中,實驗和用高速電子計算機求數值解起著重要作用。

