相關介紹
我們知道歐氏幾何與羅氏幾何的主要分歧點在於平行公理的截然相反,現在把它並列起來比較一下:
歐氏平行公理;“在平面內,過已知直線外的一個已知點,最多只能作一條直線與已知直線平行(不相交)”。
羅氏平行公理:“在平面內,過已知直線外的一個已知點,最少可以作兩條直線與已知直線不相交。”並進一步指出有無數條超平行線都與已知直線不相交。
經過比較,我們很自然地會問:是否有這樣的幾何,在平面內,過直線外的一個已知點與已知直線不相交的直線一條也沒有呢?這種“最多一條”,“最少兩條”,“一條也沒有”的聯想,必然會在人們的腦子裡反映出來。
另一種聯想是:在歐氏幾何里,三角形的內角和等於二直角;在羅氏幾何里三角形內角和小於二直角;是否有一種幾何它的三角形內角和大於二直角呢?
歷史的發展回答了這個問題。
當羅巴切夫斯基發表羅氏平行公理的論文28年後;德國數學家倍耳哈特·黎曼(Bernhard Riemann,1826-1866)在1854年發表了既不屬於歐氏也不屬於羅氏,而是自成體系的“黎曼幾何”。
黎氏平行公理:“任何兩條直線必有唯一的交點”。
同時,黎氏幾何中還指出:任何直線雖然可以任意伸長,但長度是有限的。
這個事實可以用一個歐氏的球面略加改造,作為黎氏幾何的模型來作解釋 。
基本介紹
下面是黎氏幾何模型的規定:
規定1 在歐氏空間中任取一個球面K,約定把球面上的對徑點(球直徑的兩端點)“統一起來”,看作一個對象,這個對象便叫做黎曼幾何的“點”。
規定2 球面K上的大圓叫做“黎氏直線”,大圓上的對徑點仍看作一個點。
規定3 對經點統一起來的球面K,叫做“黎氏平面”。
規定4 所謂黎氏點和黎氏直線的結合關係,就是球面K上的點與球面K上的大圓弧的普通結合關係。
由於在球面K上,任何兩個大圓必相交於兩個點,而這兩個點恰好是對徑點,把它看成一個點,所以說黎氏平面上任何兩條直線必相交於一個點,這樣就實現了黎氏平行公理 。
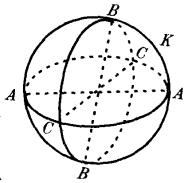 圖1
圖1 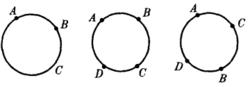 圖2
圖2 另一方面,大圓上任一點,可沿大圓弧任意移動,但大圓的長度是有限的,所以說黎氏直線可以任意伸長,但是有一定的長度。
應當注意,關於點的順序公理,必須要有所規定。因為大圓弧上的A、B、C三點。B可以在A、C之間,C可以在B、A之間;A可以在C、B之間。因此必須要用四個點,才能說明順序關係,分兩種情況說明:
1. 點對A、B分離點對C、D。意思是說,點C沿著直線移動,使之與D重合,則必須在某個時候,C與A或B重合,要使A與B重合也一樣,即A必先與C或D重合。
2. 點對A、B不分離點對C、D。這時,可以移動點C,使之與D重合,但不必通過A或B;同時也可以移動點A使與B重合,而不通過C和D。
所以必須要四個點,才能說明順序關係,直線的分離關係也是一樣。
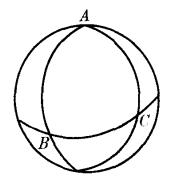 圖3
圖3 從球面幾何知識:任意三條大圓弧圍成的球面部分,稱為球面三角形(如圖ABC)。它的內角和是大於二直角的,這就證實了黎氏平面上三角形內角和大於二直角 。
我們又知道在羅巴切夫斯基平面內,三角形的面積
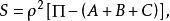 黎曼幾何模型
黎曼幾何模型 或
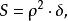 黎曼幾何模型
黎曼幾何模型 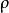 黎曼幾何模型
黎曼幾何模型 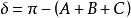 黎曼幾何模型
黎曼幾何模型 (這裡是羅氏曲率半徑,是角虧。)
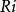 黎曼幾何模型
黎曼幾何模型 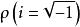 黎曼幾何模型
黎曼幾何模型 如果用換替上式中的,
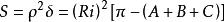 黎曼幾何模型
黎曼幾何模型 那么
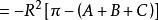 黎曼幾何模型
黎曼幾何模型 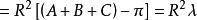 黎曼幾何模型
黎曼幾何模型 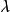 黎曼幾何模型
黎曼幾何模型 (是角余)。
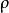 黎曼幾何模型
黎曼幾何模型 所以,在羅氏幾何中,如果把曲率半徑換成Ri的話,就得到黎氏幾何中的面積公式。這個變換不僅是十分有趣的,而且也說明了羅氏幾何和黎氏幾何之間的一種關係,給我們研究黎氏幾何開闢了一種新的途徑。
在這裡,還要指出一個十分有趣的性質:任意一條直線不能把黎曼平面分成兩個不同的區域,例如大圓a,初看似乎把球面K分成Ⅰ、Ⅱ兩部分了,似乎A點落在Ⅰ域。但不要忘記,我們是規定把A的對徑點A看成同一個點的。而這時的A是在Ⅱ區域,即A點是區域Ⅰ的點,也是區域Ⅱ的點。因此,直線a並沒有把黎曼平面分成兩個不同的區域。
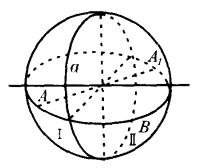 圖4
圖4 同時,我們也看到,Ⅰ、Ⅱ兩部分的點A和B,可以用不與a相交的直線段連結起來,因為A的對徑點A就是A點。很明顯,直線段AB是不與直線a相交的。
黎曼平面的這種特殊性質,用拓撲學上的名詞來說,稱為單側性。梅比烏斯帶子也是具有單側性的。
關於黎曼幾何的知識,這裡只粗略地談一些易於接受的內容,讀者如果還想進一步探討,可參閱錢端壯編著的《幾何基礎》第六章《黎曼幾何學》 。

