概述
數學規劃的經典範例是在輸入數據準確知道並且等於某些標稱值的假設條件下建立模型,並利用已有的數學規劃求解方法得到最優解。 這種方法沒有考慮數據不確定性的影響。因此, 當數據的取值不同於標稱值時, 一些約束可能不滿足,原來得到的最優解可能不再最優甚至變得不可行。因此, 需要找到一種最佳化方法使得最佳化解免受數據不確定性的影響,這種方法就是魯棒最佳化方法。
魯棒最佳化是研究不確定最佳化問題的一種新建模方法,它源自魯棒控制理論,是隨機最佳化和靈敏度分析的補充替換,其目的是尋求一個對於不確定輸入的所有實現都能有良好性能的解。該方法與隨機最佳化的不同之處在於,它沒有假設不確定參數的分布,也即是每個可能值都同等重要,當它面向最壞情況時,代表一個最保守的結果。在過去幾十年中,魯棒最佳化方法在自然科學、工程技術、經濟管理等各個領域得到了廣泛的套用和發展,深受國內外學者的關注。
原理
魯棒最佳化與其它不確定最佳化方法的最大區別在於:
①魯棒最佳化強調的是所謂的硬約束,尋求一個對於不確定輸入的所有實現都能有良好性能的解,即不確定最佳化問題的解對於任何一個可能參數的實現都必須是可行的,而其它不確定最佳化問題並沒有這個要求。
②魯棒最佳化的建模思想與其它最佳化方法不同,它是以最壞情況下的最佳化為基礎,這代表了一個保守的觀點。得到的最佳化方案並不是最優的,但是,當參數在給定的集合內發生變化時,仍能確保最佳化方案是可行的,使模型具有一定的魯棒性,即最佳化方案對參數擾動不敏感。
③魯棒最佳化對於不確定參數沒有分布假定,只是給出不確定參數集,不確定參數集合內的所有值都同等重要 。
主要方法
魯棒線性規劃;
魯棒二次規劃;
魯棒半定規劃。
適用範圍
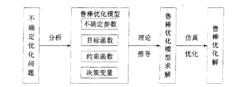 魯棒最佳化
魯棒最佳化魯棒最佳化是解決內部結構和外部環境不確定環境下的一種新的最佳化方法。魯棒最佳化解決內部結構變動問題時,主要是約束條件參數的不確定性或目標函式參數的不確定性解決外部環境變化時,主要是外界不確定性擾動。魯棒最佳化己經從最初的線性最佳化魯棒方法,發展到魯棒最佳化理論的經典體系。與其它不確定最佳化問題的處理方法不同的是,魯棒最佳化更加適用於如下情況:
①不確定最佳化問題的參數需要估計,但是有估計風險;
②最佳化模型中不確定參數的任何實現都要滿足約束函式;
③目標函式或者最佳化解對於最佳化模型的參數擾動非常敏感;
④決策者不能承擔小機率事件發生後所帶來的巨大風險。
專家學者結合各行業存在的實際問題,利用魯棒最佳化進行不確定模型研究時會採用不同的解決方式,然而研究流程大致相同 。
存在問題
魯棒最佳化作為研究不確定最佳化問題的新方法受到了越來越多學者的關注,採用事先分析的策略,在最佳化模型建立的過程中就考慮了參數的不確定性,其最佳化解的魯棒性突破了過去最佳化模型不確定參數過多依賴先驗知識以及服從機率分布的假定。儘管魯棒最佳化還未形成統一的理論體系,但正是這種百花齊放的研究思路給該領域的研究注入了活力,同時也表明該領域的研究還有許多函待解決的問題:
①在不確定集的確定上,如何與參數不確定性產生的來源和敏感級別結合起來,選擇集合的形狀和大小;
②完善並豐富初始不確定最佳化問題轉化為魯棒對等式的理論體系,使魯棒對等式為計算可處理的;
③對最佳化模型參數在其不確定集以外取值的情況加以分析,找到控制最佳化性能惡化的途徑和方法;
④推廣魯棒最佳化的套用範圍,使該理論不僅可以在經濟管理問題中得以套用,而且還可以拓展到實際的最佳化調度問題中。