定義
1950年,弗蘭克西·博伊斯在電子結構理論中首次用高斯軌道取代更多的斯萊特型軌道。在計算化學中使用高斯軌道基組的依據是 高斯乘積定理(Gaussian Product Theorem):對於兩個中心分別位於空間中兩個分隔的點上的高斯函式,它們的積可以表示為中心位於這兩個點的連線上某處的有限個高斯函式的加和。運用此方法,四中心積分可以減少為雙中心積分的有限和,下一步中減少為單中心積分的有限和。通過大幅減少基函式,高斯軌道的計算速度比斯萊特型軌道快4-5個數量級。
簡便起見,求球面高斯軌道時,許多量子化學程式在笛卡爾型高斯函式的基礎上工作,因為其容易計算,且球面函式可以用其簡單表達。
數學形式
高斯基函式遵循通常的徑向角分解:
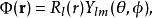 高斯軌道
高斯軌道 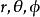 高斯軌道
高斯軌道 其中表示球諧函式, l 和 m 表示角動量及 z 軸上的分量,為球坐標。
斯萊特型軌道的徑向部分為:
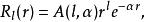 高斯軌道
高斯軌道 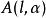 高斯軌道
高斯軌道 其中為歸一化常數。高斯軌道的徑向部分為:
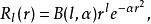 高斯軌道
高斯軌道 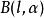 高斯軌道
高斯軌道 其中為高斯軌道的歸一化常數。
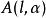 高斯軌道
高斯軌道 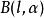 高斯軌道
高斯軌道 決定或的規範化條件為:
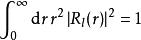 高斯軌道
高斯軌道 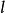 高斯軌道
高斯軌道 通常不會在中施加正交性。
單個原始高斯函式對核附近電子的波函式給出的描述很差,因此高斯軌道基組幾乎總是收縮:
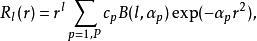 高斯軌道
高斯軌道 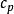 高斯軌道
高斯軌道 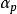 高斯軌道
高斯軌道 其中是帶指數的原函式的收縮係數。歸一化原函式的係數需要給定,因為非標準化原函式的係數有不同的數量級。指數以原子單位制報告。
分子積分
1966年,竹田等人提出了在高斯基組上獲得矩陣元素所需的數學方程。此後,做了大量工作來加快這些積分的計算,這些積分是許多量子化學計算中最慢的部分。1968年,濟夫科維奇和梅克賽奇提議使用埃爾米特-程燦高斯函式來簡化方程。1975年,麥克默里和戴維森採用了遞歸關係,大大減少了運算量。1978年,波普爾和赫雷使用了局部坐標法。1985年,奧巴拉和西卡採用了有效的遞歸關係,並發展了其它重要的遞推關係。1991年,吉爾和波普爾引入了一個“PRISM”算法,可以有效地使用20個不同的計算路徑。
POLYATOM系統
POLYATOM系統是第一個使用高斯軌道進行從頭計算的軟體,其套用於各種各樣的分子,是在麻省理工學院約翰·斯萊特的固態和分子理論組(SSMTG)中使用聯合計算實驗室的資源開發。其中,數學基礎設施和操作軟體由爾·克賽茲馬迪亞、馬爾科姆·哈里森、儒勒·莫斯科維茨及布萊恩·蘇特克里夫等人開發。
