基本含義
算題算好以後,再通過逆運算(如減法算題用加法,除法算題用乘法)演算一遍,檢驗以前運算的結果是否正確,就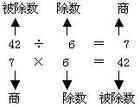 驗算
驗算是驗算。驗算能夠有效地檢查出計算過程中出現的錯誤,但對解題思維上的錯誤無太大用處,通過驗算(用結果來推導條件)所得的數據與原數據比較來建議運算是否正確。
基本方法
驗算是解決數學問題的最後一步,是一個不可缺少的環節,掌握驗算的方法,養成驗算的習慣是學好數學重要條件之一。因此在國小數學的教材中安排了一定的教學內容,如:加減法的驗算,乘除法的驗算,方程的驗算,套用題的驗算,但在平時的教學中老師對加減法的驗算,乘除法的驗算,方程的驗算比較重視,而對套用題的驗算比較輕視,這並非套用題的驗算不重要,原因之一是:因為加減法的驗算,乘除法的驗算,方程的驗算經常出現在試卷中,而套用題驗算沒有直接的出現在各類試卷中;原因之二是:加減法、乘除法、方程的驗算方法比較簡單,教師容易教,學生容易學,而套用題的驗算方法多,驗算方法又比較複雜,學生較難理解和掌握。而筆者認為讓學生掌握套用題的驗算方法比掌握加減法、乘除法、方程的驗算方法更具有價值,通過套用題的驗算對學生理解各數量之間的互逆關係、辨證關係有很大的幫助,對培養學生思維的靈活性、嚴密性有很大的促進作用,對學生的數學素養提高和良好數學習慣的養成更有不可代替的作用。
作用
驗算是對所學計算知識的鞏固和數學知識信息的再加工,培養學生的驗算能力對促進思維,發展智力,形成知識體系具有特殊的意義。驗算是計算和解決數學問題不可缺少的環節,掌握驗算的方法,養成驗算的習慣是學好數學的重要條件之一。認真驗算不僅是保證計算正確的一個有效措施,而且也可以促進學生理解數學規則,形成計算技能,同時還有助於培養學生從小就對工作認真負責的良好態度。因此,在教學中,要從學生的實際生活和知識水平出發,讓學生在具體事物中感知和理解驗算的重要意義。比如,結合作業講評、單元測驗後分析等教學活動來探究錯誤的原因,幫學生體驗“驗算”與“不驗算”的效果,使他們改變有書面要求“驗算”才驗算,沒有書面要求就不驗算的習慣,讓學生的驗算意識遷移到日後的學習和工作中。
