靜態平衡系統
在分析力學裡,虛功原理闡明,對於一個靜態平衡(staticequilibrium)系統,所有外力的作用,經過虛位移,所作的虛功,總合等於零,以方程式表達,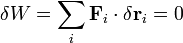 駐點
駐點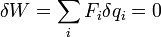 駐點
駐點假設這系統是保守系統,則每一個廣義力都是一個標量的廣義位勢函式的對於其對應的廣義坐標的導數:
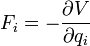 駐點
駐點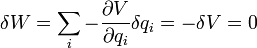 駐點
駐點歐拉-拉格朗日方程式
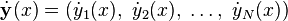 方程式
方程式主條目:歐拉-拉格朗日方程式
在變分法裡,歐拉-拉格朗日方程式是從其對應的泛函的平穩點推導出的一種微分方程式。設定參見
拐點
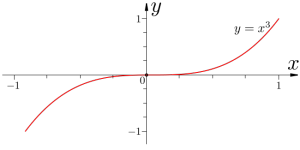
在數學上,一個反曲點或拐點是一條可微曲線改變凹凸性的點,或者等價地說,是使切線穿越曲線的點。決定曲線的拐點有助於理解曲線的外形,這在描繪曲線圖形時特別有用。
 駐點圖
駐點圖定義
 定義曲線圖
定義曲線圖拐點的充要條件
拐點的必要條件:設在內二階可導,,若是曲線的一個拐點,但是0兩側全是凸,所以0不是函式的拐點。拐點的充分條件:設在內二階可導,,若在兩側附近異號,則點為曲線的拐點。否則(即保持同號),不是拐點。
分類
拐點可以根據f'(x)為零或不為零,進行分類。如果f'(x)為零,此點為拐點的駐點,簡稱為鞍點。
如果f'(x)不為零,此點為拐點的非駐點。
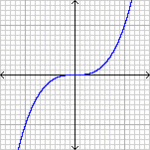
舉一個鞍點的例子,是y=x³的點(0,0)。切線為x軸;切線正好在將圖像分為兩半。
參數曲線的拐點
平面參數曲線的拐點是使其曲率變號的點,此時曲率中心(居於曲線凹側)從曲線的一側換至另一側。雙正則點與拐點
雙正則點是使得參數曲線的一階與二階微分(它們是向量)線性無關的點。在雙正則點上,曲線既無拐點亦非直線。在非雙正則點上曲率為零,但是不一定有變號。在尋找參數曲線的拐點時,我們通常先以微分找出非雙正則點,繼之研究其局部性狀,以判定是否為拐點。註:某些作者偏好將拐點定義為“使一階與二階微分平行的點”,在此定義下,切線不一定在該點穿越曲線本身。
代數曲線的拐點
設為域上的平面代數曲線,其拐點定義為一平滑點,使得該點切線與在點的相交重數。注意到一條曲線與在點相切的充要條件是相交重數。當時,代數曲線的拐點定義等價於上節註記中的廣義定義。
鞍點
一個不是局部極值點的駐點稱為鞍點。廣義而說,一個光滑函式(曲線,曲面,或超曲面)的鞍點鄰域的曲線,曲面,或超曲面,都位於這點的切線的不同邊。
 矩陣圖
矩陣圖檢驗二元實函式F(x,y)的駐點是不是鞍點的一個簡單的方法,是計算函式在這個點的黑塞矩陣:如果黑塞矩陣的行列式小於0,則該點就是鞍點。例如,函式在駐點的黑塞矩陣是:
我們可以看到此矩陣有兩個特徵值2,-2。它的行列式小於0,因此,這個點是鞍點。然而,這個條件只是充分條件,例如,對於函式點是一個鞍點,但函式在原點的黑塞矩陣是零矩陣,並不小於0。的鞍點在(0,0)
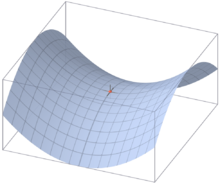
如右圖,一維鞍點看起來並不像馬鞍!在一維空間裡,鞍點是駐點·也是反曲點。因為函式圖形在鞍點由凸轉凹,或由凹轉凸,鞍點不是區域性極點。
 等高線圈圈相交叉的地點
等高線圈圈相交叉的地點兩座山中間的鞍點(雙紐線的交叉點)
思考一個擁有兩個以上變數的函式。它的曲面在鞍點好像一個馬鞍,在某些方向往上曲,在其他方向往下曲。在一幅等高線圖裡,一般來說,當兩個等高線圈圈相交叉的地點,就是鞍點。例如,兩座山中間的山口就是一個鞍點。
極值
在數學中,極大值與極小值(又被稱為極值)是指在一個域上函式取得最大值(或最小值)的點的函式值。而使函式取得極值的點(的橫坐標)被稱作極值點。這個域既可以是一個鄰域,又可以是整個函式域(這時極值稱為最值)。局部最大值:如果存在一個ε>0,使的所有滿足|x-x*|<ε的x都有f(x*)≥f(x)我們就把點x*對應的函式值f(x*)稱為一個函式f的局部最大值。從函式圖像上看,局部最大值就像是山頂。
局部最小值:如果存在一個ε>0,使的所有滿足|x-x*|<ε的x都有f(x*)≤f(x)我們就把點x*對應的函式值f(x*)稱為一個函式f的局部最小值。從函式圖像上看,局部最小值就像是山谷的底部。
全局(或稱‘絕對’)最大值:如果點x*對於任何x都滿足f(x*)≥f(x),則點f(x*)稱為全局最大值。全局(或稱‘絕對’)最小值:如果點x*對於任何x都滿足f(x*)≤f(x),則點f(x*)稱為全局最小值。
全局最值一定是局部極值,反之則不然。
極值的概念不僅僅限於定義在實數域上的函式。定義在任何集合上的實數值函式都可以討論其最大最小值。為了定義局部極值,函式值必須為實數,同時此函式的定義域上必須能夠定義鄰域。鄰域的概念使得在x的定義域上可以有|x-x*|<ε。
局部最大值(最小值)也被稱為極值(或局部最優值),全局最大值(最小值)也被稱為最值(或全局最優值)。
求極值的方法
求全局極值是最最佳化方法的目的。對於一元二階可導函式,求極值的一種方法是求駐點(亦稱為靜止點,停留點,英語:stationarypoint),也就是求一階導數為零的點。如果在駐點的二階導數為正,那么這個點就是局部最小值;如果二階導數為負,則是局部最大值;如果為零,則還需要進一步的研究。一般地,如果在駐點處的一階、二階、三階……直到N階導數都是零,而N+1階導數不為零,則當N奇數且N+1階導數為正時,該點為極小值;當N是奇數且N+1階導數為負時,該點為極大值;如果N是偶數,則該點不是極值。
如果這個函式定義在一個有界區域內,則還要檢查局域的邊界點。如果函式在定義域記憶體在不可導點,則這些不可導點也可能是極值點。
例子
函式有惟一最小值,在x=0 處取得。函式沒有最值,也沒有極值,儘管其一階導數在x=0處也為0。因為其二階導數(6x)在該點也是0,但三階導數不是零。函式cos(x)有無窮多個最大值,在x=0,±2π,±4π,...,與無窮多個最小值 在x=±π,±3π....
求函式的極值時還應當考慮其不可導點,即導數不存在的點。如函式y=|x|中0處的導數不存在,事實上從圖像上也能看出這一點來。而且0就是該函式的一個極小值。
![駐點[數學概念] 駐點[數學概念]](/img/7/79a/nBnauM3XwIjM1YTMygDN2IDOxQTMwUjMyMDN0MTNwAzMwIzL4QzLwczLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg)
