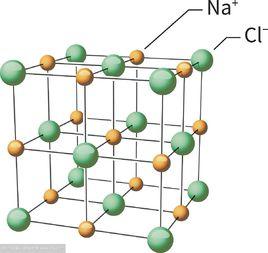
推算
若用U表示離子i和j之間的相互作用能，則可定義一個和式U，讓其包括所有涉及第i個離子的相互作用，即有
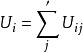馬德隆能式中求和包括除j=i以外的所有離子。如果U可以寫成 λexp(-r/ρ) 形式的中心場排斥勢與庫侖勢 ±q/r 之和(λ、ρ均為經驗參數),那么在CGS單位制中有:
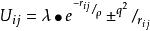馬德隆能式中對同號電荷取“+”號，對異號電荷取“-”號
若略去表面效應，則可以把N個分子（或2N個離子）所組成的晶體的總晶格能量U寫成U=NU 。注意：這個式子中出現的是N，而不是2N，這是因為對於每個相互作用對或每個鍵只能計算一次。
引入量p，使r=p ijR，其中R為晶體中的最近鄰間距，如果只計及最近鄰間的排斥相互作用，便有
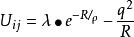馬德隆能（最近領）
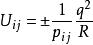馬德隆能(除最近鄰以外)
於是，
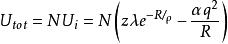馬德隆能式中，z是任一離子的最近領數，並且定義α為馬德隆常數
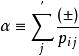馬德隆能在達到平衡間距時，有dU/dR=0，由此導出
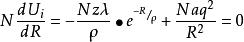馬德隆能或
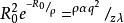馬德隆能由此式可知，如果排斥相互作用的兩個參數ρ和λ已知，則可得到平衡間距R；則包含2N個離子的晶體在其平衡間距為R時的總晶格能寫為
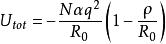馬德隆能其中-Nαq /R為馬德隆能量。
其他
馬德隆能表征了離子晶體中的結合能，其中馬德隆常數在離子晶體理論中有著非常重要的作用。
