簡介
餘弦相似性通過測量兩個向量的夾角的餘弦值來度量它們之間的相似性。0度角的餘弦值是1，而其他任何角度的餘弦值都不大於1；並且其最小值是-1。從而兩個向量之間的角度的餘弦值確定兩個向量是否大致指向相同的方向。兩個向量有相同的指向時，餘弦相似度的值為1；兩個向量夾角為90°時，餘弦相似度的值為0；兩個向量指向完全相反的方向時，餘弦相似度的值為-1。這結果是與向量的長度無關的，僅僅與向量的指向方向相關。餘弦相似度通常用於正空間，因此給出的值為0到1之間。
注意這上下界對任何維度的向量空間中都適用，而且餘弦相似性最常用於高維正空間。例如在信息檢索中，每個詞項被賦予不同的維度，而一個維度由一個向量表示，其各個維度上的值對應於該詞項在文檔中出現的頻率。餘弦相似度因此可以給出兩篇文檔在其主題方面的相似度。
另外，它通常用於文本挖掘中的檔案比較。此外，在數據挖掘領域中，會用到它來度量集群內部的凝聚力。
定義
兩個向量間的餘弦值可以通過使用歐幾里得點積公式求出：
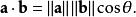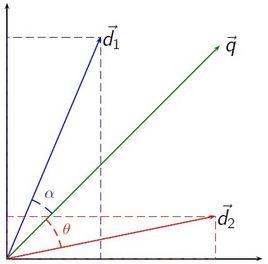
餘弦相似度給定兩個屬性向量， A和 B，其餘弦相似性 θ由點積和向量長度給出，如下所示：
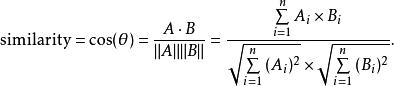餘弦相似度
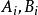餘弦相似度這裡的分別代表向量A和B的各分量。
給出的相似性範圍從-1到1：-1意味著兩個向量指向的方向正好截然相反，1表示它們的指向是完全相同的，0通常表示它們之間是獨立的，而在這之間的值則表示中間的相似性或相異性。
對於文本匹配，屬性向量 A和 B通常是文檔中的詞頻向量。餘弦相似性，可以被看作是在比較過程中把檔案長度正規化的方法。
在信息檢索的情況下，由於一個詞的頻率（TF-IDF權）不能為負數，所以這兩個文檔的餘弦相似性範圍從0到1。並且，兩個詞的頻率向量之間的角度不能大於90°。
角相似性
“餘弦相似性”一詞有時也被用來表示另一個係數，儘管最常見的是像上述定義那樣的。透過使用相同計算方式得到的相似性，向量之間的規範化角度可以作為一個範圍在[0,1]上的有界相似性函式，從上述定義的相似性計算如下：
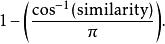餘弦相似度這式子適用於向量係數可以為正或負的情況。
或者，用以下式子計算
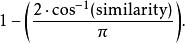餘弦相似度這式子適用於向量係數總為正的情況。
雖然“餘弦相似性”一詞有時會用來表示這個角距離，但實際上很少這樣說，因為角度的餘弦值只是作為一種計算角度的簡便方法而被用到，本身並不是意思的一部分。角相似係數的優點是，當作為一個差異係數（從1減去它）時，產生的函式是一個嚴格距離度量，而對於第一種意義的“餘弦相似性”則不然。然而，對於大多數的用途，這不是一個重要的性質。若對於某些情況下，只有一組向量之間的相似性或距離的相對順序是重要的，那么不管是使用哪個函式，所得出的順序都是一樣的。
與“Tanimoto”係數的混淆
有時，餘弦相似性會跟一種特殊形式的、有著類似代數形式的相似係數相混淆：
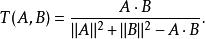餘弦相似度事實上，這個代數形式是首先被Tanimoto定義，作為在所比較集合由位元向量表示時計算其Jaccard係數的方法。雖然這公式也可以擴展到向量，它具有和餘弦相似性頗為不同的性質，並且除了形式相似外便沒有什麼關係。
Ochiai係數
這個係數在生物學中也叫Ochiai係數，或Ochiai-Barkman係數：
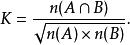餘弦相似度這裡A和B是集合，n(A)是A的元素個數。如果集合由位元向量所代表，那么可看到Ochiai係數跟餘弦相似性是等同的。
性質
餘弦值的範圍在[-1,1]之間，值越趨近於1，代表兩個向量的方向越接近；越趨近於-1，他們的方向越相反；接近於0，表示兩個向量近乎於正交。
套用
最常見的套用就是計算文本相似度。將兩個文本根據他們詞，建立兩個向量，計算這兩個向量的餘弦值，就可以知道兩個文本在統計學方法中他們的相似度情況。實踐證明，這是一個非常有效的方法。
另見
•Sorensen相似性指數
•漢明距離
•相關
•Dice係數
•Jaccard指數
•SimRank
•信息檢索
