基本介紹
定義 設W是線性空間V的一個子空間,如果V還有一個子空間W',滿足:
V=W+W',W∩W' ={0},
我們就把W'叫做是W的一個 餘子空間。
此時, 我們說V是子空間W與W'的直和, 並記作:
V = W⊕W'.
很明顯,如果W'是W的一個餘子空間,那么W也是W'的一個餘子空間。
子空間的和子空間的和是子空間的一種運算,設V是域P上的線性空間,V,V,…,V是V的子空間,若:
S={α+α+…+α|α∈V,i=1,2,…,s},
則S是V的子空間,稱為子空間V,V,…,V的和,記為V+V+…+V;子空間V,V,…,V的集合交V∩V∩…∩V也是V的子空間,稱為V,V,…,V的交,設dim V=n,ε,ε,…,ε是V的基,若V是V的子空間,則dim V≤n,當dim V<n,及ε′,ε′,… ,ε′為V的基時,必存在ε′,…,ε′使ε′,ε′,…,ε′為V的基,由ε′,…,ε′生成的子空間V稱為V的餘子空間(或補子空間)。V與它的餘子空間V的和V+V=V,它們的交V∩V={0},此時,又稱V為V與V的直和 。
相關結論
n維線性空間V的任意一個子空間W的餘子空間W'總是存在的。如果W=V,那么W'={0};如果W={0},那么W' =V 。
如果W是V的一個真子空間。取W的一個基
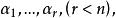 餘子空間
餘子空間把它擴充成V的基
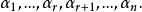 餘子空間
餘子空間我們有
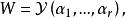 餘子空間
餘子空間令
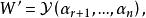 餘子空間
餘子空間那么
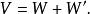 餘子空間
餘子空間現在證明W∩W'={0}。設ξ∈W∩W'。那么
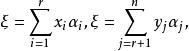 餘子空間
餘子空間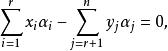 餘子空間
餘子空間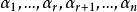 餘子空間
餘子空間由於 線性無關。不難看出
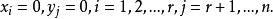 餘子空間
餘子空間於是ξ= 0,從而W∩W'={0}。所以
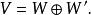 餘子空間
餘子空間此時還有:
dimW + dimW' = dimV.
然而,n維線性空間V的一個真子空間W的餘子空間並不唯一。例如,在三維幾何空間V中,過原點的一個平面W是V的一個二維子空間。而過原點但不在W上的任何一條直線L都是W的一個餘子空間。這是因為
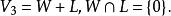 餘子空間
餘子空間所以
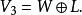 餘子空間
餘子空間定理設線性空間V能寫成子空間W與W'的直和,那么V中每一個向量ξ都可以唯一地表成
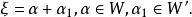 餘子空間
餘子空間數域F上每一個n階矩陣都可以表成一個對稱矩陣與一個反對稱矩陣的和,並且表法是唯一的。
關於直和的概念還可以推廣到多於兩個子空間的情形。
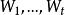 餘子空間
餘子空間設 是線性空間V的子空間。 如果
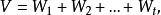 餘子空間
餘子空間且
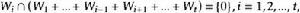 餘子空間
餘子空間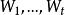 餘子空間
餘子空間就把V叫做是子空間 的直和,並記作
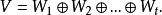 餘子空間
餘子空間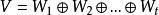 餘子空間
餘子空間可以證明, 如果 ,那么V中每一個向量ξ都可唯一地表成
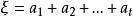 餘子空間
餘子空間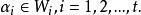 餘子空間
餘子空間的形式, 其中
並且當V是有限維線性空間時,還有 :
dimV=dimW₁+dimW₂+... + dimW.