詳細介紹
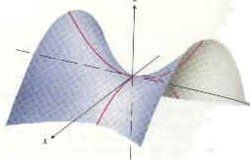
廣義而說，一個光滑函式(曲線，曲面，或超曲面)的鞍點鄰域的曲線，曲面，或超曲面，都位於這點的切線的不同邊。
參考右圖，鞍點這詞來自於不定二次型x2-y2的二維圖形，像馬鞍:x-軸方向往上曲，在y-軸方向往下曲。
檢驗二元是函式F(x，y)的駐點是不是鞍點的一個簡單的方法，是計算函式在這個點的黑塞矩陣:如果黑塞矩陣的行列式小於0，則該點就是鞍點。例如:函式z = x2 − y2在駐點(0，0)的黑塞矩陣是:
|2 0 |
|0 -2|
我們可以看到此矩陣有兩個特徵值2，-2。它的行列小於0，因此，這個點是鞍點。然而，這個條件只是充分條件，例如，對於函式z = x4 − y4,點(0,0)是一個鞍點，但函式在原點的黑塞矩陣是零矩陣，並不小於0。如右圖，一維鞍點看起來並不像馬鞍!在一維維空間裡，鞍點是駐點.也是反曲點點。因為函式圖形在鞍點由凸轉凹，或由凹轉凸，鞍點不是區域性極點。
思考一個只有一個變數的函式。這函式在鞍點的一次導數等於零，二次導數換正負符號.例如，函式y=x3就有一個鞍點在原點。
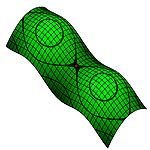兩座山中間的鞍點思考一個擁有兩個以上變數的函式。它的曲面在鞍點好像一個馬鞍，在某些方向往上曲，在其他方向往下曲。在一幅等高線圖裡，一般來說，當兩個等高線圈圈相交叉的地點，就是鞍點。例如，兩座山中間的山口就是一個鞍點。
C語言求鞍點代碼
#include " stdio.h"
#include " conio.h"
#include "malloc.h"
#define TRUE 1
#define FALSE 0
#define OK 0
#define ERROR 1
#define MAXX 80
void Print(int * const pMatrix, const int m, const int n);
void Input(const int * const pm, const int * const pn);
void CreatTureMatrix(int ** const pMatrix,int ** const pTrueMatrixconst, const int m, const int n);
OutPrint(int ** const pMatrix, int ** const pTrueMatrix, const int m, const int n );
int main(void)
{
system("cls");
{
const int m = FALSE, n = FALSE;
Input(&m, &n);
{
int * pMatrix = NULL, * pTrueMatrix = NULL;
CreatTureMatrix(&pMatrix, &pTrueMatrix, m, n);
printf("\nMatrix is :\n");
Print(pMatrix, m , n);
printf("\nSaddle point Ture Matrix is :\n");
Print(pTrueMatrix, m, n);
OutPrint(&pMatrix, &pTrueMatrix, m, n);
}
}
getch();
return (OK);
}
void Print(int * const pMatrix, const int m, const int n)
{
int * p = NULL;
for(p = pMatrix; p < pMatrix + m*n; ++p)
{
printf("%5d", *p);
if( !( (p - pMatrix)%n- (n-1) ) )
{printf("\n"); }
}
}
void Input(const int * const pm,const int * const pn)
{
printf("Please enter a matrix of rows, columns: ");
{
int flag = TRUE;
while(flag)
{
if(scanf("%d%d", pm, pn) - 2)
{
flag = TRUE;
printf("Worry enter,retry!\n");
fflush(stdin);
}
else if( (*pm<=0 || *pm>=10) && (*pn<=0) || (*pn>=10) )
{
flag = TRUE;
printf("Enter Big or small,retry!\n");
}
else
{flag = FALSE;}
}
}
}
void CreatTureMatrix(int ** const pMatrix,int ** const pTrueMatrix, const int m, const int n)
{
*pMatrix = (int *)malloc( m*n*sizeof(int) );
*pTrueMatrix = (int *)calloc( m*n,sizeof(int) );
{
int *p = NULL;
for(p = *pMatrix; p < *pMatrix + m*n; ++p)
{scanf("%d",p);}
}
{
int * p = NULL;
for(p = *pMatrix; p < *pMatrix + m*n; p += n)
{
int * pMaxj = p;
{
int * q = NULL;
for(q = p + 1; q < p + n; ++q)
{
if(*q > *pMaxj)
{pMaxj = q;}
}
}
{
int * q = NULL;
for(q = pMaxj; q < p + n; ++q) /*此處處理所有（不嚴格）最大值*/
{
if( !(*q - *pMaxj) )
{
int * r = NULL;
for(
r = *pMatrix + (q - *pMatrix)%n
;(r < *pMatrix + m*n) && (*r >= *pMaxj)
;r += n
);
if( r >= (*pMatrix + m*n) )
{*(*pTrueMatrix + (q - *pMatrix)) = 1; }
}
}
}
}
}
}
OutPrint(int ** const pMatrix, int ** const pTrueMatrix, const int m, const int n )
{
int count = 0;
int * p = NULL;
printf("\nSaddle point is :\n");
for(p = *pTrueMatrix; p < *pTrueMatrix + m*n; ++p)
{
if(*p)
{
printf("Matrix[%d][%d] = %3d, "
, (p - *pTrueMatrix)/n, (p - *pTrueMatrix)%n
, *(*pMatrix + (p - *pTrueMatrix)) );
++count;
}
}
free(*pMatrix);
*pMatrix = NULL;
free(*pTrueMatrix);
*pTrueMatrix = NULL;
if(count)
{
const int xPos = wherex(), yPos = wherey();
if(xPos - 1)
{gotoxy(xPos - 2, yPos); }
else
{gotoxy(MAXX - 1, yPos - 1); }
printf(".");
} /*此處TC一類特有的函式gotoxy（）*/
else
{printf("It is not exist!\n"); }
}
