簡介
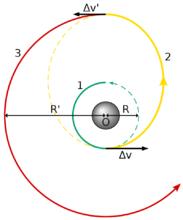圖1.霍曼轉移軌道為圖中編號2的半橢圓軌道右圖為將太空船從低軌道（1）送往較高軌道（3）的霍曼轉移軌道。太空船在原先軌道（1）上瞬間加速後，進入一個橢圓形的轉移軌道（2）。太空船由此橢圓軌道的近拱點開始，抵達遠拱點後再瞬間加速，進入另一個圓軌道（3），此即為目標軌道。要注意的是，三個軌道的軌道半長軸是越來越大，因此兩次引擎推進皆是加速，總能量增加而進入較高（半長軸較大）的軌道。
反過來，霍曼轉移軌道亦可將太空船送往較低的軌道，不過是兩次減速而非加速。
霍曼轉移軌道的兩次加速假設是瞬間完成，但實際上加速要花時間，因此需要額外的燃料來補償。使用高推力引擎所需額外燃料較小，低推力引擎則還要以控制推進時間、逐漸提高軌道來逼近霍曼轉移軌道。因此實際上ΔV會比假設情況更大且花更多時間。
計算
軌道上物體的總能等於動能與重力位能的和，而總能又等於重力位能（軌道半徑為軌道半長軸a時的重力位能）的一半：
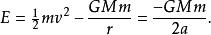霍曼轉移軌道以速度為未知解方程式，得到軌道能量守衡方程式：
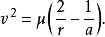霍曼轉移軌道
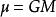霍曼轉移軌道其中，v為物體的速度，為中央物體的標準重力參數，r為物體至中央物體中心的距離，a為物體軌道的半長軸。
因此霍曼轉移所需的兩次ΔV為（假設速度改變是瞬間達成）：
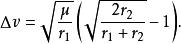霍曼轉移軌道
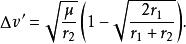霍曼轉移軌道
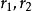霍曼轉移軌道分別是原本圓軌道與目標圓軌道的半徑，其中大的（小的）對應到霍曼轉移軌道的遠拱點（近拱點）距離。
無論前往較高或較低軌道，根據克卜勒第三定律，霍曼轉移所花的時間為：
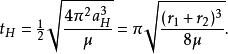霍曼轉移軌道
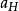霍曼轉移軌道（即橢圓軌道周期的一半），其中是霍曼轉移軌道的半長軸。
