研究進程
早在30 年代就開始用磁感應電場加速電子的初步探討和實驗。
到1940 年克斯特(D.W.Kerst)建成了第一台電子感應加速器，把電子加速到2.3 MeV。
1945 年在這種加速器上已能得到能量為100MeV 的電子。在電子感應加速器的研製過程中提出了電子的振盪理論，並解決了帶電粒子在加速過程中的穩定性問題。這個理論適用於各種類型常梯度磁場聚焦的加速器。
因此在加速器的發展史上，電子感應加速器起了重要的作用。
從60 年代發展起來的直線感應加速器，這類加速器不但能加速電子，還能加速離子，近20 年來發展很快，目前，己能提供能量為幾十MeV、脈衝電流為數kA 的電子束流，在很多新的科研領域中得到了套用。
原理
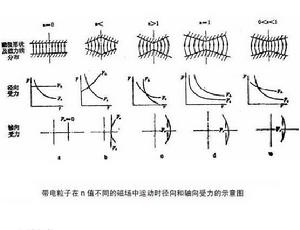
把帶電粒子送入軌道的過程稱為注入過程。粒子源每秒鐘要將大量粒子注入到加速器中，其中絕大多數粒子不能注入到封閉軌道上，它們的運動方向也並不沿著“封閉軌道”的切線方向。這些粒子注入後，在0<n<1 的常梯度磁場中受軸向和徑向聚焦力的作用而圍繞封閉軌道振盪．
這種沒有外力作用，僅由於初始偏離封閉軌道而引起的橫向振盪稱為自由振盪．又因自由振盪最早是在電子感應加速器上研究的，所以又稱為電子感應加速器振盪。
電子感應加速器振盪方程
粒子在常梯度磁場中的徑向和軸向自由振盪方程是：
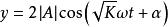電子感應加速器振盪式中
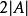電子感應加速器振盪——振盪振幅；
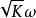電子感應加速器振盪——振盪角頻率；
電子感應加速器振盪——是初始相角。
電子感應加速器振盪頻率
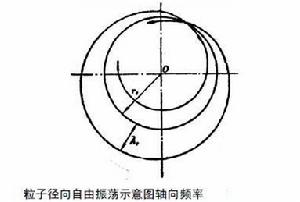
電子感應加速器振盪在常梯度磁場中，因為0<n<1，所以粒子沿‘封閉軌道”轉一圈，自由振盪還不到一次．右圖是粒子圍繞封閉軌道徑向自由振盪的示意圖。圖中Ax 表示徑向振盪的振幅。
由振盪方程得出：
（1）軸向自由振盪頻率
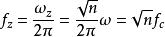電子感應加速器振盪（2）徑向自由振盪頻率
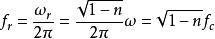電子感應加速器振盪式中
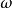電子感應加速器振盪——粒子迴旋的角頻率；
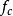電子感應加速器振盪——粒子沿封閉軌道的迴旋頻率。
電子感應加速器振盪振幅
1、電子感應加速器振盪的振幅由初始條件決定。初始條件有二：
（1）注入粒子的位置偏離“封閉軌道”，即當t=0 時：
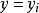電子感應加速器振盪
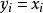電子感應加速器振盪
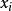電子感應加速器振盪
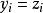電子感應加速器振盪
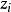電子感應加速器振盪討論徑向運動時 ， 為初始時徑向偏離值；對於軸向運動 ， 為初始時軸向偏離值。
（2）注入時離子的運動方向偏離封閉軌道的切線方向，即t=0 時，
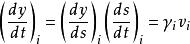電子感應加速器振盪式中
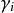電子感應加速器振盪——初始時粒子運動方向對封閉軌道切線的偏角；
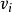電子感應加速器振盪——粒子沿封閉軌道運動的初始速度。
2、再根據振盪方程可以得出
（1）初始時徑向電子感應加速器振盪振幅為：
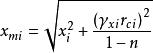電子感應加速器振盪
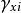電子感應加速器振盪式中 為初始時粒子的徑向偏角。
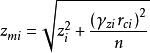電子感應加速器振盪（2）初始時軸向電子感應加速器振盪振幅為：
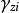電子感應加速器振盪式中 為初始時粒子的軸向偏角。
電子感應加速器振盪振幅的衰減
前面在求解自由振盪方程時，曾假設m、K、ω 都是常數。但實際上，在加速過程中帶電粒子的質量是隨時間緩慢變化的．在環型軌道的加速器中，為了保持軌道半徑不變，磁場也是隨時間而變化的，也就是說粒子的質量m、角頻率ω、以及磁場B 和磁場梯度n 都隨時間而變化，即m（t）、ω（t）、B（t）、K（t）。變化的結果將引起自由振盪振幅的衰減。
