算法 和程式
雷諾方程解法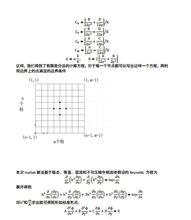
雷諾方程解法clc;clear;clf
D=0.04; %軸頸半徑
R=D/2;
c=0.00008; %半徑間隙 單位m
D2=0.04016; %軸承內徑
L=0.1; %軸承長度
l=0.003; % 內襯厚度
u=0.001005; %水的粘度 Pa.s
namda=1.2 ; %鬆弛因子
omiga=600*2*pi/60; % 自轉轉速 r/min--rad/s
E=10000000; %內襯pa
v=0.49; % 泊松比
v0=sqrt(2*v^2/(1-v)); %當量泊松比
%% 設定參數
e=0.6; %軸頸偏心率
x=0; % 特定情況下的軸心位置
y=-c*e;
vx=0; %渦動速度為0 靜態力求解
vy=0;
pq=1; % 氣體壓力，油膜破裂準則
p0=0; % 壓力初值
m=60; %軸向等分數；
n=60; % 周向等分數；
%% 對z歸一化採用 z=ZR 軸向坐標軸對稱分布z=(-L/2,L/2)
deltL=2*(L/2/R)/m; %軸向等分間距
deltsita=2*pi/n; %周向角度等分大小
%% 邊界條件及各處p的初值
% 初始狀態P和H
%%
ERR=1.0e-5; %誤差
PK=zeros(n+1,m+1); %各點賦初值
k=1; %疊代計數
while k>0
P=PK; %下次疊代賦值
%% 計算各點處水膜厚度
for i=1:n+1 %周向
for j=1:m+1 %軸向
H(i,j)=1+e*(cos((i-1)*deltsita))+6*l*(1-v0.^2)*u*omiga*R.^2./(E*c.^3).*P(i,j);
end
end
%% 疊代係數 參見文獻公式
for i=2:n
for j=2:m
aa(i,j)=H(i,j)^2*(H(i,j)-3/4*(H(i+1,j)-H(i-1,j)))/(deltsita^2);
bb(i,j)=H(i,j)^2*(H(i,j)+3/4*(H(i+1,j)-H(i-1,j)))/(deltsita^2);
cc(i,j)=-2*H(i,j)^3*(1/(deltsita^2)+1/(deltL^2));
dd(i,j)=H(i,j)^2*(H(i,j)-3/4*(H(i,j+1)-H(i,j-1)))/(deltL^2);
ee(i,j)=H(i,j)^2*(H(i,j)+3/4*(H(i,j+1)-H(i,j-1)))/(deltL^2);
% f(j,i)=(H(j,i+1)-H(j,i-1))/(2*deltsita)+2*(-VY*cos(deltsita*(i-1))+VX*sin(deltsita*(i-1)));
ff(i,j)=(H(i+1,j)-H(i-1,j))/(2*deltsita); %不考慮軸心渦動 只計算該瞬態的穩定壓力分布
end
end
%% 疊代過程計算
for i=2:n
for j=2:m
% PK(i,j)=(1-namda)*P(i,j)+namda*(ff(i,j)-(aa(i,j)*P(i-1,j)+bb(i,j)*P(i+1,j)+dd(i,j)*P(i,j-1)+ee(i,j)*P(i,j+1)))/cc(i,j); %加速收斂
PK(i,j)=(ff(i,j)-(aa(i,j)*P(i-1,j)+bb(i,j)*P(i+1,j)+dd(i,j)*P(i,j-1)+ee(i,j)*P(i,j+1)))/cc(i,j);
if PK(i,j)<0
PK(i,j)=0; %油膜破裂 置零
break;
end
end
end
%% 誤差控制
sum1=0;
sum2=0;
for s=1:n+1
for t=1:m+1
sum1=sum1+abs((PK(s,t)-P(s,t)));
sum2=sum2+abs(P(s,t));
end
end
sum=sum1/sum2;
if sum<=ERR
break;
end
k=k+1
%% 遍歷各處 i ,j
end
VV=6.*u.*omiga.*2.*pi./60.*R.^2./c.^2 %恢復成有量綱壓力時的比例計算
% P=P.*VV; % 恢復成有量綱量
sitas=(0:n)*deltsita; %周向
Ls=(0:m)*(L/m); %軸向
[SITA,LL]=meshgrid(sitas,Ls);
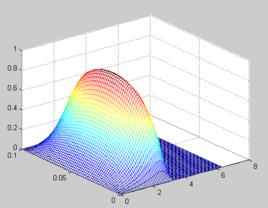
mesh(SITA,LL,P')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 數值積分求等效力
Fx=0;
Fy=0;
for i=1:n+1
for j=1:m+1
Fx=Fx+P(i,j)*sin((i-1)*deltsita)*deltsita*deltL;
Fy=Fy-P(i,j)*cos((i-1)*deltsita)*deltsita*deltL;
end
end
fx=6.*u.*omiga*R.^4./c.^2*Fx
fy=6.*u.*omiga*R.^4./c.^2*Fy
f=sqrt(fx^2+fy^2)
theta=180/pi*atan(fy/fx)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 數值積分求等效力矩
Mx=0;
My=0;
for i=1:n+1
for j=1:m+1
Mx=Mx-P(i,j)*(deltL*(m/2+1-j))*cos((i-1)*deltsita)*deltsita*deltL;%P前面的符號將所有的力轉換成沿x,y軸的正向；(m/2+1-j)的符號決定Z向坐標的正負
My=My+P(i,j)*(deltL*(j-m/2-1))*sin((i-1)*deltsita)*deltsita*deltL;
end
end
mx=6.*u.*omiga*R.^5./c.^2*Mx
my=6.*u.*omiga*R.^5./c.^2*My
m=sqrt(mx^2+my^2)
theta=180/pi*atan(my/mx)
