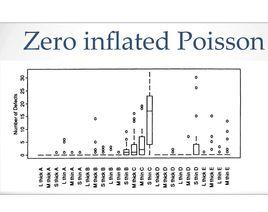
簡介
例如保險索賠次數,索賠數為0的機率很高,否則保險公司就面臨破產風險。這種數據數資料中的零值過多,超出了Poisson分布等一般離散分布的預測能力。零膨脹這個概念首先是由Lambert在1992年的論文“Zero-Inflated Poisson Regression,with an Application to Defects in Manufacturing”中提出。
零膨脹泊松
第一個零膨脹模型是Diane Lambert的零膨脹泊松模型,該模型涉及在單位時間內包含過量零計數數據的隨機事件。例如,某些類型風險的人口中的保險索賠數量將由那些沒有針對風險購買保險而因此無法提出索賠的人實現零膨脹。零膨脹泊松(ZIP)模型採用兩個對應於兩個零生成過程的組件。第一個過程由生成結構零的二進制分布控制。第二個過程由泊松分布控制,該分布生成計數,其中一些可能為零。兩個模型組件描述如下:
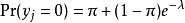 零膨脹模型
零膨脹模型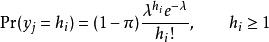 零膨脹模型
零膨脹模型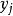 零膨脹模型
零膨脹模型 零膨脹模型
零膨脹模型 零膨脹模型
零膨脹模型 零膨脹模型
零膨脹模型結果變數 具有任何非負整數值, 是 個體的預期泊松計數; 是額外零的機率。
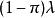 零膨脹模型
零膨脹模型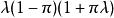 零膨脹模型
零膨脹模型平均值為 ,方差為 。
ZIP的估算
矩估計的方法由下式給出
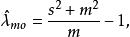 零膨脹模型
零膨脹模型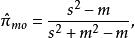 零膨脹模型
零膨脹模型 零膨脹模型
零膨脹模型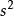 零膨脹模型
零膨脹模型其中 是樣本均值, 是樣本方差。
最大似然估計可以通過求解以下等式找到
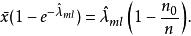 零膨脹模型
零膨脹模型。
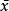 零膨脹模型
零膨脹模型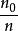 零膨脹模型
零膨脹模型其中 是樣本均值,是觀察到的零比例。
 零膨脹模型
零膨脹模型這可以通過疊代來解決,並且的最大似然估計由下式給出:
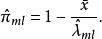 零膨脹模型
零膨脹模型。
相關模型
1994年,格林考慮了零膨脹負二項式(ZINB)模型。Daniel B. Hall將Lambert的方法套用於上限計數情況,從而獲得零膨脹二項式(ZIB)模型。
離散偽複合泊松模型
 零膨脹模型
零膨脹模型如果計數數據具有零機率的特徵大於非零機率,即
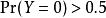 零膨脹模型
零膨脹模型 零膨脹模型
零膨脹模型那么離散數據遵循離散偽複合Poisson分布。
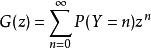 零膨脹模型
零膨脹模型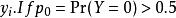 零膨脹模型
零膨脹模型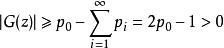 零膨脹模型
零膨脹模型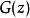 零膨脹模型
零膨脹模型實際上,讓是{\ displaystyle y_ {i}} y_ {i}的機率生成函式。如果,則。然後從Wiener-Lévy定理我們證明具有離散偽複合泊松分布的機率生成函式。
 零膨脹模型
零膨脹模型我們說離散隨機變數滿足機率生成函式表征
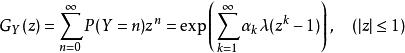 零膨脹模型
零膨脹模型具有參數的離散偽複合泊松分布
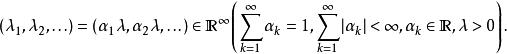 零膨脹模型
零膨脹模型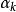 零膨脹模型
零膨脹模型當所有都是非負數時,它是具有過度離散屬性的離散複合泊松分布(非泊松情形)。