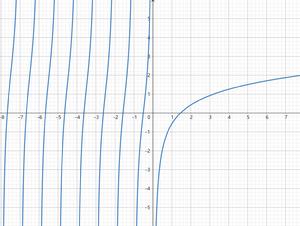
第一個多伽瑪函式
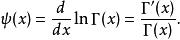雙伽瑪函式與調和數的關係
雙伽瑪函式，通常用ψ0(x)、ψ(x)或 F來表示，與調和數有以下的關係：
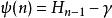雙伽瑪函式其中Hn是第n個調和數，γ是歐拉-馬歇羅尼常數。對於半整數的值，它可以表示為：
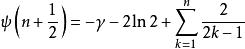雙伽瑪函式積分表示法
它有以下的積分表示法：
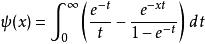雙伽瑪函式也可以寫為
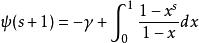雙伽瑪函式這可以從調和數的歐拉積分公式得出。
泰勒級數
雙伽瑪函式有一個有理ζ級數，由z=1的泰勒級數給出。這是
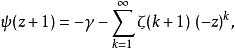雙伽瑪函式當|z|<1時收斂。在這裡，{\displaystyle \zeta (n)}是黎曼ζ函式。這個級數可以很容易從赫爾維茨ζ函式的泰勒級數推導出。
牛頓級數
雙伽瑪函式的牛頓級數可從歐拉積分公式得出：
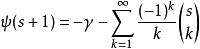雙伽瑪函式其中{\displaystyle \textstyle {s \choose k}}是二項式係數。
反射公式
雙伽瑪函式滿足一個反射公式，類似於伽瑪函式的反射公式：
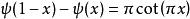雙伽瑪函式遞推關係
雙伽瑪函式滿足以下的遞推關係：
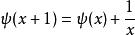雙伽瑪函式高斯和
雙伽瑪函式具有以下形式的高斯和：
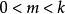雙伽瑪函式
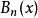雙伽瑪函式其中m是整數，且 。在這裡，ζ(s,q)是赫爾維茨ζ函式， 是一個伯努利多項式。乘法定理的一種特殊情況是：
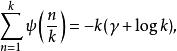雙伽瑪函式一個推廣為：
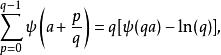雙伽瑪函式其中假設了q是自然數，而1-qa則不是。
高斯雙伽瑪定理
雙伽瑪函式
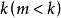雙伽瑪函式對於正整數 和 ，雙伽瑪函式可以用初等函式來表示：
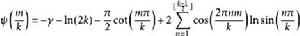雙伽瑪函式近似公式
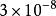雙伽瑪函式
雙伽瑪函式誤差約為 ，結果越靠近 誤差越大。
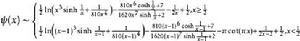雙伽瑪函式特殊值
雙伽瑪函式有以下的特殊值：
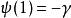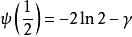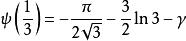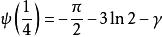雙伽瑪函式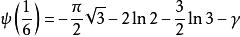
雙伽瑪函式
雙伽瑪函式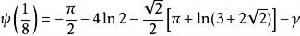
雙伽瑪函式
雙伽瑪函式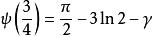
雙伽瑪函式
雙伽瑪函式參見
•伽瑪函式
•三伽瑪函式
•多伽瑪函式
