定義
我們以前經常接觸的函式,其表達式大多是自變數的某個算式,如
 隱函式組
隱函式組 隱函式組
隱函式組這種形式的函式稱為顯函式. 但在不少場合會遇到另一種形式的函式,其自變數與因變數之間的對應法則是由一個方程式所確定,通常稱為隱函式。 例如: 。
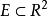 隱函式組
隱函式組 隱函式組
隱函式組設,函式 。對於方程
 隱函式組
隱函式組 隱函式組
隱函式組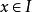 隱函式組
隱函式組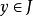 隱函式組
隱函式組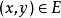 隱函式組
隱函式組 隱函式組
隱函式組 隱函式組
隱函式組如果存在集合 ,對任何 ,有惟一確定的 ,使得 ,且滿足方程(1),則稱方程(1)確定了一個定義在上,值域含於 的隱函式。若把它記為
 隱函式組
隱函式組則成立恆等式
 隱函式組
隱函式組例如方程
 隱函式組
隱函式組 隱函式組
隱函式組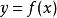 隱函式組
隱函式組 隱函式組
隱函式組能確定一個定義在 上的隱函式 。如果從方程中把 解出,這個函式也可表示為顯函式形式
 隱函式組
隱函式組設有方程組
 隱函式組
隱函式組 隱函式組
隱函式組 隱函式組
隱函式組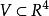 隱函式組
隱函式組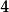 隱函式組
隱函式組 隱函式組
隱函式組 隱函式組
隱函式組其中 , 為定義在 上的 元函式。 若存在平面區域 ,對於中
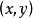 隱函式組
隱函式組 隱函式組
隱函式組 隱函式組
隱函式組的每一點 ,有惟一的 ,使得 ,且滿足方程(2)確定了 隱函式組
 隱函式組
隱函式組 隱函式組
隱函式組並在 上成立恆等式
 隱函式組
隱函式組定理
 隱函式組
隱函式組 隱函式組
隱函式組 隱函式組
隱函式組 隱函式組
隱函式組 隱函式組
隱函式組 隱函式組
隱函式組為了探索由方程組(2)確定的隱函式組所需要的條件,不妨假設(2)中的函式 和 是可微的,而且由(2)所確定的兩個隱函式 和 也是可微的。那么通過對方程組(2)關於,分別求偏導數,得到
 隱函式組
隱函式組 隱函式組
隱函式組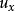 隱函式組
隱函式組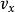 隱函式組
隱函式組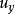 隱函式組
隱函式組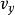 隱函式組
隱函式組要想從(3)中解出 與 ,從(4)中解出 與 ,其充分條件是它們的係數行列式不為零,即
 隱函式組
隱函式組 隱函式組
隱函式組 隱函式組
隱函式組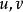 隱函式組
隱函式組 隱函式組
隱函式組(5)式左邊的行列式稱為函式 , 關於變數 的函式行列式(或雅克比(Jacobi)行列式)亦可記作 。
隱函式定理
 隱函式組
隱函式組 隱函式組
隱函式組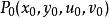 隱函式組
隱函式組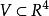 隱函式組
隱函式組若 與 在以點 為內點的區域 上滿足
 隱函式組
隱函式組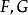 隱函式組
隱函式組(i)在 上 具有一階連續偏導數,
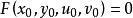 隱函式組
隱函式組 隱函式組
隱函式組(ii) , (初始條件),
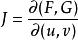 隱函式組
隱函式組 隱函式組
隱函式組(iii) 在點 不等於零,
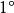 隱函式組
隱函式組 隱函式組
隱函式組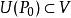 隱函式組
隱函式組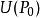 隱函式組
隱函式組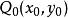 隱函式組
隱函式組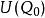 隱函式組
隱函式組則 存在點 的某一(四維空間)鄰域 ,在 上,方程組(2)惟一地確定了定義在點 的某一(二維空間)鄰域 上的兩個二元隱函式
 隱函式組
隱函式組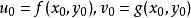 隱函式組
隱函式組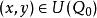 隱函式組
隱函式組使得 ,且當 時
 隱函式組
隱函式組 隱函式組
隱函式組 隱函式組
隱函式組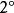 隱函式組
隱函式組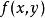 隱函式組
隱函式組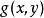 隱函式組
隱函式組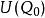 隱函式組
隱函式組, 在 上連續;
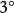 隱函式組
隱函式組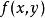 隱函式組
隱函式組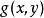 隱函式組
隱函式組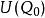 隱函式組
隱函式組, 在 上有一階偏導數,且
 隱函式組
隱函式組 隱函式組
隱函式組