概念
降維法是把一個多因素問題轉化成一個較少因素(降低問題的維數)問題,而且較容易進行合理安排,找到最優點或近似最優點,以期達到滿意的試驗結果的方法。主要類型有縱橫對摺法、等高線法和平行線法。
分類與介紹
依安排試驗步驟的差異,降維法可分為縱橫對摺法、等高線法和平行線法。下面主要介紹一下常用的等高線法。
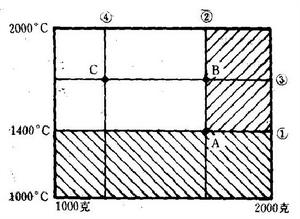 圖1
圖1等高線法
第一步是根據經驗,把一個因素固定在適當的位置上。如無經驗可憑,可先把一個因素固定在它的選值範圍的0.618處。然後對第二個因素進行優選。第二個因素選到較好的點就將第二個因素暫時固定,對第一個因素進行優選。這樣交替進行最優逼近,直到取得滿意的結果為止。
以熔煉特種鋼,對溫度因素和特殊元素加入量因素進行優選為例,說明等高線法的套用。 已知溫度的範圍是1000—2000℃;某元素的加入量是1000—2000克。見圖1 依經驗先把溫度固定在1400℃。在直線①上對元素加入量進行單因素優選,得到最好點A;再在過A點的直線②上對溫度進行優選得到②上的最好點B;沿著A所在直線①捨去不含B點的範圍,再通過B點做直線③,在③上對加入量進行優選,找到③上的最好點C;再沿著B所在直線②捨去不含C點的範圍。如此繼續下去,在過C點的直線④上選擇最佳溫度……,直到取得滿意結果為止。
等高線法是雙因素降維法較常用的一種適用性較普遍的一種方法。
縱橫對摺法
縱橫對摺法是與等高線法相似,但每次取值都在取值範圍的1/2處(類似對分法)的一種雙因素降維法。
平行線法
平行線法是適用於兩因素中有一因素不易調變的情況。按單因素的0.618法在不易調變的因素上取值,並將其固定,再對另一因素按單因素優選法優選,得到最優值後,比較取捨。見圖2
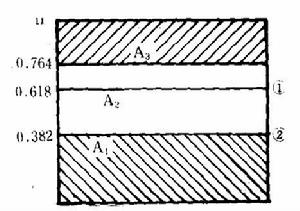 圖2
圖2流程
降維法的流程如下:
(1)把立體圖形轉化為平面圖形
把立體圖形轉化為平面圖形需要稍許空間想像力,可參考圖形推理中的摺紙盒問題提升相應的能力。行測考試中,需要轉化為平面圖形的立體圖形一般比較規則,多是立方體或四面體。
(2)把問題對應在平面圖形下就是把原問題對應在轉化後的平面圖形下。
示例:求立體圖形兩點間沿外表面的最短路徑,在把立體圖形展開為平面圖後,就是求平面上對應點間的最短路徑。
(3)用平面幾何知識求解
即對化簡後的平面問題用平面幾何知識分析求解。
適用範圍
在考試中,降維法主要套用於立體圖形的幾何問題,利用這個方法,把立體圖形轉化為平面圖形,降低題目難度。
例題分析
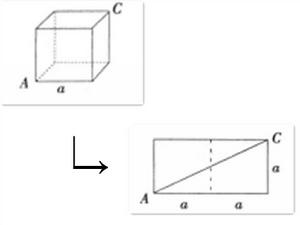
一隻螞蟻從3圖的正方體A頂點沿正方體的表面爬到正方體C頂點。設正方體邊長為a,問該螞蟻爬過的最短路程為多少?
 圖3
圖3解析:
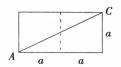 圖4
圖4把表面展開,將A與C置於同一平面中,如圖4所示只有一種展開方式。
原問題中涉及兩個頂點A、C,那么展開後原問題簡化為求平面圖上A、C兩點之間的最短路徑。
在同一平面上,兩點之間的線段最短,因此計算AC的長度:
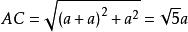 降維法
降維法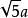 降維法
降維法即最短路徑為 。