基本原理
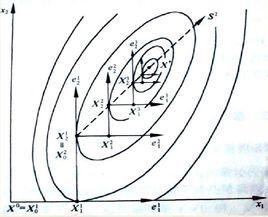
坐標輪換法或叫變數輪換法,又稱降維法,它的每次搜尋只允許在一個變數上進行,其餘變數保持不變,即它是把一個n維無約束最最佳化問題轉化為依次沿相應的n個坐標軸方向的一維最最佳化問題,並反覆進行若干輪循環疊代來求解的直接搜尋方法。
 坐標輪換法
坐標輪換法 坐標輪換法
坐標輪換法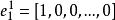 坐標輪換法
坐標輪換法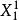 坐標輪換法
坐標輪換法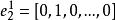 坐標輪換法
坐標輪換法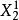 坐標輪換法
坐標輪換法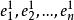 坐標輪換法
坐標輪換法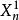 坐標輪換法
坐標輪換法對於n維無約束最佳化問題,先將(n-1)個變數固定不動,只變化第一個變數 ,即由起始點第一個變數 的方向 進行一維搜尋,得到好點 ;而後再保持(n-1)個變數不變,對第二個變數進行一維搜尋,此時搜尋方向為 ,得到好點 。如此沿 方向(即坐標方向),且將前一次一維搜尋的好點作為本次一維搜尋的好點作為本次一維搜尋的起始點,依次進行一維搜尋後,完成一輪計算。若未收斂,則以前一輪的末點 為起始點,進行下一輪的循環,如此一輪一輪疊代下去,直到滿足收斂準則,逼近最優點為止。
疊代步驟
具體疊代步驟如下:
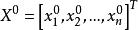 坐標輪換法
坐標輪換法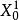 坐標輪換法
坐標輪換法(1)任選初始點 作為第一輪的起點 ,置n個坐標軸方向矢量為單位坐標矢量:
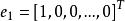 坐標輪換法
坐標輪換法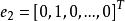 坐標輪換法
坐標輪換法 坐標輪換法
坐標輪換法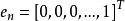 坐標輪換法
坐標輪換法(2)按照下面疊代公式進行疊代計算:
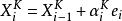 坐標輪換法
坐標輪換法式中,K為疊代輪數的序號,K=1,2,...,i 是該輪中一維搜尋的序號,依次取i=1,2,3等。步長一般通過一維最佳化求出其最優步長。
(3)按下式判別是否該終止疊代:
 坐標輪換法
坐標輪換法若滿足,疊代終止,並輸出最優解:
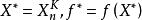 坐標輪換法
坐標輪換法疊代步長確定
疊代步長a的確定常用下述兩種方法之一:
(1)最優步長。在沿坐標軸方向的搜尋中,利用一維最佳化方法來確定沿該方向上具有最小目標函式值的步長。
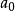 坐標輪換法
坐標輪換法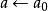 坐標輪換法
坐標輪換法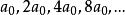 坐標輪換法
坐標輪換法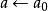 坐標輪換法
坐標輪換法(2)加速步長。先選擇一個不大的初始步長,在每次一維搜尋中都是先沿正向從開始作試探計算函式值,若函式值下降,則以倍增的速度加大步長,步長序列為,直到函式值保持下降的最後一個步長為止。若試探時函式值已增大,則改沿反向,即取後再加速步長。
優缺點
優點
坐標輪換法的優點是不需要確定目標函式的解析式,也不用求解目標函式的導數;方法簡單,易於理解。它屬於“爬山法”的一種,尋優過程猶如爬山,步步登高(目標函式值步步降低),找到了最優點(函式值最小),就好比登上了山的頂峰。
缺點
應當看到,由於它的疊代過程沒有對變數做任何的比較評價(當然,這也正是它的優點),所以它的疊代過程帶有很大的盲目性。對於維數不多的最佳化問題,此法具有很大的優越性;但對於高維最佳化問題,如溫度場中的換熱係數,此法就變得效率很低了 。
特點
(1)方法結構簡單,易於掌握,但計算效率低,對維數較高的最佳化問題更為突出,通常用於低維最佳化問題;
(2)本方法的收斂效果在很大程度上取決於目標函式等值線的形狀。