陀螺穩定性

研究陀螺力對力學系統的影響，進而建立某些判別系統穩定性的準則，為分析工程技術問題提供必要的理論依據。 具有高速轉動的旋轉對稱型部件的儀器叫做陀螺儀。陀螺儀可以裝配在固定基座上或運動機座（如飛機、火箭和衛星）上工作。由多個陀螺儀和有關的元部件組成的系統稱為陀螺系統。 在含有陀螺儀的系統的運動方程中，會出現速度的線性項，這些項的係數矩陣是反對稱的。如果把這些項視為力，它們就是理論研究中通常所說的陀螺力（或稱為陀螺項）；這種力在系統的實位移上所做功的和等於零。陀螺力不僅出現在含有陀螺儀的系統中，而且也出現在許多不含陀螺儀的力學系統和物理系統中，如自旋衛星的陀螺效應和不變磁場對運動電子的作用力也都具有陀螺力的性質，因此，用陀螺力的觀點來研究問題具有更廣泛的意義。 學者們早就發現，旋轉物體的陀螺現象是宇宙間一種常見的自然現象。天文學家們很早就發現地球的地軸具有經常指向北極星的特性，後來又發現地軸的指向還在作兩種有規則的周期運動：進動和章動（見剛體定點轉動解法），這就是地球的陀螺現象。可見，地球本身就是一個帶有液體的大陀螺。陀螺儀在工程技術上的套用始於18世紀中葉，當時在航海技術上雖也做過試驗，但還沒有造出真正適用的陀螺儀。直至20世紀初才有了較完善的陀螺儀。近幾十年來，各種高精度、長壽命，大過載的慣性元件和比較精密的陀螺系統，已經在航海、航空和航天中得到了廣泛的套用（見陀螺平台慣性導航系統）。

研究方法

對於含有陀螺儀的系統和雖不含陀螺儀但具有陀螺力的系統，它們的運動方程可以用（第二類）拉格郎日方程描述。在工程技術上，通常套用線性化方程並結合實驗方法和數字仿真技術進行分析。因此，可把描述保守系統的拉格朗日方程的線性近似變換為簡正坐標的形式：

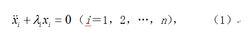陀螺穩定性

這是一個二階常係數線性方程組，式中 x是簡正坐標。方程（1）的零解（ x=0， x=0，…， x=0）是系統的平衡狀態。如果取零解為無擾運動，方程（1）即為對應的受擾運動微分方程（見運動穩定性）。將方程（1）積分，可得：

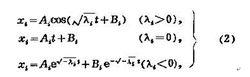陀螺穩定性

式中 A、 B（ i=1，2，…， n）為積分常數。由式（2）可知：當全部λ>0時，平衡狀態穩定；而當有λ=0或λ <0時，則不穩定。因為λ的符號直接影響著平衡狀態的穩定性，所以就稱它們為穩定係數。在λ中取負值的個數稱為不穩定度。當所有穩定係數都不取零值時，就稱平衡狀態是孤立的。

為了進一步研究系統穩定性，還需引進瑞利耗散函式，其函式式為：

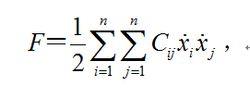陀螺穩定性

式中 C為阻尼係數，為簡正坐標對時間的導數。如果這個二次型函式含有一切簡正坐標的導數（這個函式是正定二次型），就稱為完全耗散：否則就稱為部分耗散。與它們對應的力分別稱為完全耗散力和部分耗散力。

開爾文-泰特-切塔耶夫定理 這是一個有關陀螺力和耗散力對保守系統平衡狀態穩定性影響的定理，它包含下面一些主要結論：如果保守系統的平衡狀態是穩定的（穩定係數皆為正），則當附加陀螺力和部分耗散力（或無耗散力）後，平衡狀態仍然穩定；而當附加陀螺力和完全耗散力後，平衡狀態變為漸近穩定。如果孤立的平衡狀態不穩定（穩定係數皆不為零，且至少有一個為負），則當附加陀螺力和完全耗散力後，平衡狀態仍不穩定。如果孤立的平衡狀態不穩定，且不穩定度是奇數（穩定係數皆不為零，而有奇數個負值），則在附加陀螺力後，平衡狀態仍不穩定。如果不穩定度不是奇數，則當附加適當的陀螺力後，平衡狀態可以變為穩定。因此，對於孤立不穩定的平衡狀態，要實現系統的陀螺穩定，不穩定度應該不是奇數，而且沒有附加的完全耗散力。

上述定理是首先由開爾文和泰特等人提出，後又由切塔耶夫利用里雅普諾夫定理作了嚴格的證明。近年來，這一定理由於在航空和航天中的套用，受到廣泛的重視。雖然定理中用的是線性命題，而且只針對保守系統的孤立平衡狀態，但在一定條件下，有些結論也可以推廣到非線性的情況。可是，對於保守系統的非孤立平衡狀態（此時，有的穩定係數取為零），穩定性問題的分析就比較困難。此外，陀螺力和耗散力對於非保守系統穩定性的影響也值得研究，因為這些問題在新技術中也經常出現。

參考文獻

1、詞條作者：王照林．《中國大百科全書》74卷（第一版）力學 詞條：陀螺儀系統穩定性：中國大百科全書出版社，1987 ：485-486頁．